Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có :
![]()
![]()
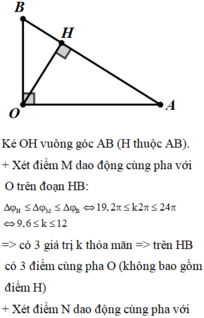
Gọi H là chân đường cao kẻ từ O xuống AB
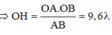
Xét đoạn AH : để cùng pha O thì ![]() với
với ![]()
![]()
Xét đoạn BH : để cùng pha O thì ![]() với
với ![]()
Vậy tất cả có : 7 + 3 = 10 giá trị của k , tức có 10 vị trí cùng pha với O ( tính cả hai điểm A,B).

Đáp án D
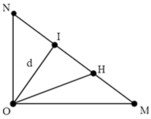
Gọi I là một điểm bất kì nằm trên MN
Độ lệch pha dao động giữa nguồn và I là:
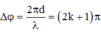
![]()
Gọi H là trung điểm của MN, khi đó dựa vào tính chất của tam giác vuông ta có
![]()
Số điểm dao động ngược pha với O trên đoạn NH:

![]()
→ Có 5 điểm.
Số điểm dao động ngược pha với O trên đoạn MH:
![]()
![]()
→ Có 1 điểm.
Vậy có tất cả 6 điểm dao động ngược pha với O trên đoạn MN
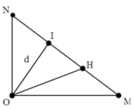

+ Gọi OH là đường cao kẻ từ O đến MN.
+ Ta có:

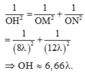
+ Những điểm dao động ngược pha với O thỏa mãn điều kiện:

+ Vậy tổng trên MN có 6 điểm dao động ngược pha với O. => Chọn C.
Chú ý: Cách giải này cũng áp dụng cho các loại bài cùng hoặc lệch pha bất kì.

Đáp án C
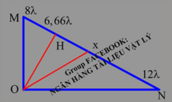
Gọi OH là đường cao kẻ từ O đến MN
Ta có: 1 O H 2 = 1 O M 2 + 1 O N 2 = 1 8 λ 2 + 1 12 λ 2
⇒ O H ≈ 6 , 66 λ
Những điểm dao động ngược pha với O thỏa mãn điều kiện: x = k + 0 , 5 λ
Đi từ H đến M có 1 điểm 7 , 5 λ
Đi từ H đến N có 7 , 5 λ ; 8 , 5 λ ; 9 , 5 λ ; 10 , 5 λ ; 11 , 5 λ
Vậy tổng trên MN có 6 điểm dao động ngược pha với O
Chú ý: Cách giải này cũng áp dụng cho các loại bài cùng hoặc lệch pha bất kì

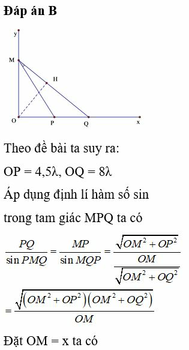
Đáp án B
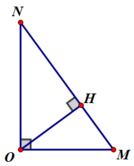
Kẻ OH vuông góc với MB. Áp dụng hệ thức lượng:

Để dao động ngược pha với O thì độ lệch pha phải là số lẻ lần π . Như vậy ta có :
+ Trên NH : độ lệch pha từ 13,32 π đến 24 π , như vậy có các điểm ngược pha là 15, 17, 19, 21, 23.
+ Trên HM : độ lệch pha từ 13,32 π đến 16 π , vậy có điểm ngược pha 15.
Vậy trên MN tổng cộng có 6 điểm ngược pha O.






Chọn A.