Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

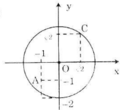
Gọi R là bán kính của đường tròn O: R = 2
Ta có:
OA2 = 12 + 12 = 2 => OA = √2 < R
=> A nằm bên trong (O)
OB2 = 12 + 22 = 5 => OB = √5 > R
=> B nằm bên ngoài (O)
OC2 = (√2)2 + (√2)2 = 4 => OC = 2 = R
=> C nằm trên (O)

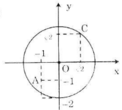
Gọi R là bán kính của đường tròn O: R = 2
Ta có:
OA2 = 12 + 12 = 2 => OA = √2 < R
=> A nằm bên trong (O)
OB2 = 12 + 22 = 5 => OB = √5 > R
=> B nằm bên ngoài (O)
O C 2 = ( √ 2 ) 2 + ( √ 2 ) 2 = 4 = > O C = 2 = R
=> C nằm trên (O)

Chọn đáp án C
Ta có: 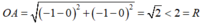
Nên A nằm trong đường tròn tâm O bán kính R = 2

Gọi R là bán kính của đường tròn (O; 2). Ta có: R = 2
O A 2 = 1 2 + 1 2 = 2 ⇒ OA = 2 < 2
Vì OA < R nên điểm A nằm trong đường tròn (O; 2)
O B 2 = 2 2 + 2 2 = 2 + 2 = 4 ⇒ OB = 2
Vì OB = R nên điểm B thuộc đường tròn (O; 2)
O C 2 = 1 2 + 2 2 = 1 + 4 = 5 ⇒ OC = 5 > 2

Ta có:
\(\sqrt{2016a+\frac{\left(b-c\right)^2}{2}}=\sqrt{2016a+\frac{b^2-2bc+c^2}{2}}=\sqrt{2016a+\frac{b^2+2bc+c^2-4bc}{2}}\)
\(=\sqrt{2016a+\frac{\left(b+c\right)^2-4bc}{2}}=\sqrt{2016a+\frac{\left(b+c\right)^2}{2}-2bc}\)
\(\le\sqrt{2016a+\frac{\left(b+c\right)^2}{2}}\left(b,c\ge0\right)=\sqrt{2016a+\frac{\left(a+b+c-a\right)^2}{2}}\)
\(=\sqrt{2016a+\frac{\left(1008-a\right)^2}{2}}=\sqrt{\frac{\left(1008+a\right)^2}{2}}=\frac{1008+a}{\sqrt{2}}\left(a\ge0\right)\)
Tương tự cho 2 BĐT còn lại ta cũng có:
\(\sqrt{2016b+\frac{\left(c-a\right)^2}{2}}\le\frac{1008+b}{\sqrt{2}};\sqrt{2016c+\frac{\left(a-b\right)^2}{2}}\le\frac{1008+c}{\sqrt{2}}\)
Cộng theo vế 3 BĐT trên ta có:
\(VT\le\frac{3\cdot1008+\left(a+b+c\right)}{\sqrt{2}}=\frac{4\cdot1008}{\sqrt{2}}=2016\sqrt{2}\)

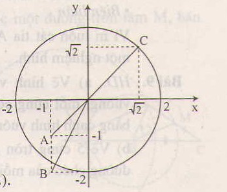
Khoảng cách d từ gốc tọa độ đến điểm (x;y) được tính theo công thức d=√x2+y2d=x2+y2
Ta có OA=√2<2⇒AOA=2<2⇒A nằm trong đường tròn (O;2).
OB=√5>2⇒BOB=5>2⇒B nằm ngoài đường tròn (O;2).
OC=2⇒COC=2⇒C nằm trên đường tròn (O;2).