Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi các điểm nằm giữa 2 đường thẳng $x=-10; x=50$ có tọa độ $(a,b)$
Ta có:
$-10< a< 50(1)$
Tung độ $b=\frac{8a+6}{13}$ là số nguyên nên $8a+6\vdots 13$
$\Rightarrow 5(8a+6)\vdots 13$
$\Rightarrow 13(3a+2)+a+4\vdots 13\Rightarrow a+4\vdots 13$
$\RIghtarrow a=13k-4$ với $k$ nguyên.
$\Rightarrow -10< 13k-4< 50\Rightarrow 0\leq k\leq 4$
$k=0\Rightarrow a=-4; b=-2$
$k=1\Rightarrow a=9; b=6$
$k=2\Rightarrow a=22; b=14$
$k=3\Rightarrow a=35; b=22$
$k=4\Rightarrow a=48; b=30$
Vậy.......
Lời giải:
Gọi các điểm nằm giữa 2 đường thẳng $x=-10; x=50$ có tọa độ $(a,b)$
Ta có:
$-10< a< 50(1)$
Tung độ $b=\frac{8a+6}{13}$ là số nguyên nên $8a+6\vdots 13$
$\Rightarrow 5(8a+6)\vdots 13$
$\Rightarrow 13(3a+2)+a+4\vdots 13\Rightarrow a+4\vdots 13$
$\RIghtarrow a=13k-4$ với $k$ nguyên.
$\Rightarrow -10< 13k-4< 50\Rightarrow 0\leq k\leq 4$
$k=0\Rightarrow a=-4; b=-2$
$k=1\Rightarrow a=9; b=6$
$k=2\Rightarrow a=22; b=14$
$k=3\Rightarrow a=35; b=22$
$k=4\Rightarrow a=48; b=30$
Vậy.......

- a) Thay x=-1;y=3 vào (d) ta có: 3=(m+2)-1-m+6 <=>-m-2-m+6=3 <=>-2m=-1 <=>m=1/2.

(đơn vị đo trên các trục tọa độ là xentimet)
Lời giải:
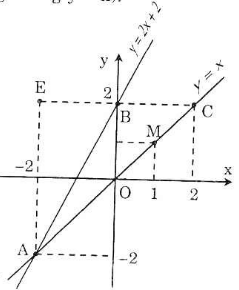
a) Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x. Vẽ đường thẳng qua B(0; 2) và E(-1; 0) được đồ thị hàm số y = 2x + 2.
b) Tìm tọa độ của điểm A: giải phương trình 2x + 2 = x, tìm được x = -2. Từ đó tìm được x = -2, từ đó tính được y = -2, ta có A(-2; -2).
c) Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.
a) Đồ thị hàm số \(y=x\) là 1 đường thẳng đi qua 2 điểm O \(\left(0;0\right)\) và E\(\left(1;1\right)\)
Đồ thị hàm số \(y=2x+2\) là 1 đường thẳng đi qua 2 điểm B \(\left(0;2\right)\) và D \(\left(-1;0\right)\)
b) Hoành độ giao điểm A của 2 đường thẳng đã cho là nghiệm của pt:
\(x=2x+2\)
\(\Leftrightarrow\) \(x-2x=2\)
\(\Leftrightarrow\) \(-x=2\)
\(\Leftrightarrow\) \(x=-2\)
Tại \(x=-2\) thì giá trị của y là: \(y=2.\left(-2\right)+2=-2\)
Vậy tọa độ điểm A \(\left(-2;-2\right)\)
c) Đường thẳng song song với trục tung Ox và cắt trục hoành tại điểm B(0;2)
\(\Rightarrow\) Suy ra phương trình đường thẳng có dạng \(y=2x\)
Hoành độ giao điểm C của 2 đường thẳng y=2x và y=x là nghiệm của pt: 2x=x
\(\Rightarrow\) Tọa độ điểm C (2;2)
\(S_{ABC}=S_{ADO}+S_{BCOD}\)

a) Vẽ tương đối (d1), (d2)
O y x 6 -4 d1 -1 -3 d2
b) Phương trình hoành độ giao điểm của (d1) và (d2):
\(\frac{3}{2}\)\(x+6\)\(=\) \(-3x-3\)
\(\Leftrightarrow\)\(\frac{9}{2}\)\(x=\)\(-9\)
\(\Leftrightarrow\)\(x=\)\(-2\)
\(\Rightarrow\)\(y=3\)
Vậy giao điểm của (d1) và (d2) là \(\left(-2;3\right)\)
c) Gọi phương trình đường thẳng cần tìm là (d): y = ax + b
(d) // (d1) => (d):\(\frac{3}{2}\) \(x+b\)
A \(\in\)(d2) => A \((\)\(\frac{-4}{3}\)\(;1\)\()\)
Thay tọa độ A vào đường thẳng (d) ta có :
1 = \(\frac{3}{2}\) .\(\frac{-4}{3}\)+ b
\(\Leftrightarrow\)b = 3
Vậy (d): y =\(\frac{3}{2}\) \(x+3\)
:3