Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

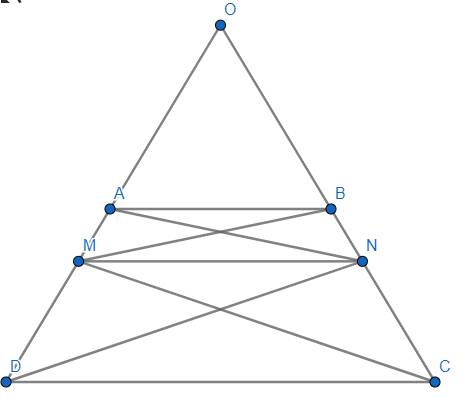
(a) Cho \(AD\cap BC=\left\{O\right\}.\) Do \(AB\left|\right|CD\left(gt\right)\Rightarrow\hat{OAB}=\hat{ODC}=\hat{OCD}=\hat{OBA}\) (đồng vị và tính chất hình thang cân) \(\Rightarrow\Delta OAB\) cân tại \(O\Rightarrow OA=OB.\)
Mà: \(AM=BN\Rightarrow OA+AM=OB+BN\Leftrightarrow OM=ON\Rightarrow\Delta OMN\) cân tại \(O\Rightarrow\hat{OMN}=\hat{ONM}=\dfrac{180^o-\hat{O}}{2}\left(1\right)\).
Lại có \(\Delta OAB\) cân tại \(O\left(cmt\right)\Rightarrow\hat{OAB}=\hat{OBA}=\dfrac{180^o-\hat{O}}{2}\left(2\right)\)
Từ (1) và (2), suy ra: \(\hat{OMN}=\hat{OAB}\Rightarrow AB\left|\right|MN\).
Mà: \(AB\left|\right|CD\left(gt\right)\Rightarrow AB\left|\right|MN\left|\right|CD\left(3\right)\)
Từ (1) và (3) \(\Rightarrow ABNM\) là hình thang cân (đpcm).
Mặt khác: \(\hat{MDC}=\hat{NCD}\left(gt\right)\left(4\right)\)
Từ (3) và (4) \(\Rightarrow MNCD\) là hình thang cân (đpcm).

a: ABCD là hình chữ nhật
=>\(AC^2=AB^2+AD^2\)
=>\(AC^2=256+81=337\)
=>\(AC=\sqrt{337}\left(cm\right)\)
b: Sửa đề: MA=NB
Xét ΔMAD vuông tại A và ΔNBC vuông tại B có
MA=NB
AD=BC
Do đó: ΔMAD=ΔNBC
=>\(\widehat{MDA}=\widehat{NCB}\)
\(\widehat{ADM}+\widehat{MDC}=90^0\)
\(\widehat{NCB}+\widehat{NCD}=90^0\)
mà \(\widehat{MDA}=\widehat{NCB}\)
nên \(\widehat{MDC}=\widehat{NCD}\)
Xét tứ giác MNCD có MN//CD và \(\widehat{MDC}=\widehat{NCD}\)
nên MNCD là hình thang cân

Bài khá dài đó.
Sorry nhé mik mới lớp 6 ak nên ko bít, tha lỗi nha!
ý kiến gì thì nhắn tin cho mik mai 7g
pp, ngủ ngon!
 cảm ơn bạn và cho mik hỏi là làm thế này có đc ko
cảm ơn bạn và cho mik hỏi là làm thế này có đc ko
Xét Δ ADM và Δ BNC ta có :
Góc A = Góc B = 90o (ABCD là HCN)
AD=BC (ABCD là HCN)
AM=BN (đề bài)
⇒ Δ ADM và Δ BNC (cạnh, góc, cạnh)
⇒ Góc ADM = Góc BCN
mà Góc ADM + Góc MDC =90o
Góc BCN + Góc NCD =90o
⇒ Góc MDC = Góc NCD
mà MN song song CD (AB song song CD)
⇒ MNCD là hình thang cân