
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+) Số trung bình: \(\overline x = \frac{{0.10 + 1.30 + 2.40 + 3.20}}{{100}} = 1,7\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm, \(\underbrace {0,...,0}_{10},\underbrace {1,...,1}_{30},\underbrace {2,...,2}_{40},\underbrace {3,...,3}_{20}.\)
Bước 2: Vì \(n = 100\), là số chẵn nên \({Q_2} = \frac{1}{2}(2 + 2) = 2\)
\({Q_1}\) là trung vị của nửa số liệu: \(\underbrace {0,...,0}_{10},\underbrace {1,...,1}_{30},\underbrace {2,...,2}_{10}.\) Do đó \({Q_1} = \frac{1}{2}(1 + 1) = 1\)
\({Q_3}\) là trung vị của nửa số liệu \(\underbrace {2,...,2}_{30},\underbrace {3,...,3}_{20}.\) Do đó \({Q_3} = \frac{1}{2}(2 + 2) = 2\)
+) Mốt \({M_o} = 2\)

Để chắc chắn lấy ra được ba bóng màu đỏ chúng ra cần xem xét khả năng xấu nhất chưa lấy ra được ba bóng màu đỏ: Toàn bộ bóng xanh và bóng vàng được lấy ra, do đó bắt buộc phải thêm 3 bóng đỏ nữa, và câu trả lời là cần lấy ra 28 bóng (28 = 15 + 10 + 3) thì chắc chắn có 3 bóng đỏ.
Đầu tiên phải lấy tổng số bóng xanh và bóng vàng ra
=> Cần phải lấy \(15+10=25\left(q\right)\)
Sau đó chỉ cần lấy thêm 3 quả nữa là chắc chắn có 3 quả mầu đỏ
=> Cần phải lấy \(25+3=28\left(q\right)\)

Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega \right) = C_{13}^2.13\)
a) Biến cố “Ba quả bóng lấy ra cùng màu” xảy ra khi hai lần đều lấy ra bóng có cùng màu xanh, đỏ hoặc vàng. Số kết quả thuận lợi cho biến cố là \(C_5^2.5 + C_6^2.6 + C_2^2.2 = 142\)
Vậy xác suất của biến cố “Ba quả bóng lấy ra cùng màu” là \(P = \frac{{142}}{{13C_{13}^2}} = \frac{{71}}{{507}}\)
b) Số kết quả thuận lợi cho biến cố “Bóng lấy ra lần 2 là bóng xanh” là \(C_{13}^2.5\)
Vậy xác suất của biến cố “Bóng lấy ra lần 2 là bóng xanh” là \(P = \frac{{5C_{13}^2}}{{13C_{13}^2}} = \frac{5}{{13}}\)
c) Biến cố “Ba bóng lấy ra có ba màu khác nhau” xảy ra khi hai quả bóng lấy ra lần đầu là 2 màu khác nhau và quả bóng lấy lần 2 có màu còn lại. Số kết quả thuận lợi cho biến cố này là \(5.6.2.3 = 180\)
Vậy xác suất của biến cố “Ba bóng lấy ra có ba màu khác nhau” là \(P = \frac{{180}}{{13C_{13}^2}} = \frac{{30}}{{169}}\)
Cái này nhân 3 TH thui
VD (xanh+đỏ; vàng) ; (xanh+vàng; đỏ); (đỏ+vàng;xanh) nên x3 chứ không phải nhân 3! á em (câu c)

a) Biến cố: “Bi lấy ra có màu xanh hoặc đen hoặc trắng” là biến cố: “Không xảy ra H” do đó là biến cố \(\overline H \).
b) \(\overrightarrow K \) là biến cố: “Không xảy ra K” tức là biến cố: “Bi lấy ra có màu đỏ hoặc màu đen”. Do đó biến cố: “Bi lấy ra màu đen” không phải là biến cố \(\overline K \).

+) Mỗi lần lấy ngẫu nhiên ra 4 bông hoa từ 30 bông hoa ta có một tổ hợp chập 4 của 30. Do đó số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{30}^4\) (phần tử)
+) Gọi A là biến cố “ bốn bông hoa chọn ra có cả ba màu”
+) Để chọn ra bốn bông hoa có đủ 3 màu ta chia ra làm ba trường hợp:
TH1: 2 bông trắng, 1 bông vàng, 1 bông đỏ: \(C_{10}^2.10.10\) (cách chọn)
TH2: 1 bông trắng, 2 bông vàng, 1 bông đỏ: \(10.C_{10}^2.10\) (cách chọn)
TH3: 1 bông trắng, 1 bông vàng, 2 bông đỏ: \(10.10.C_{10}^2\) (cách chọn)
+) Áp dụng quy tắc cộng, ta có \(n\left( A \right) = 13500\) ( cách chọn)
+) Xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{100}}{{203}}\)

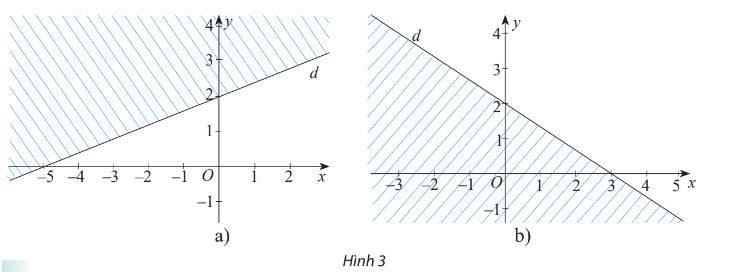
Gọi phương trình đường thẳng \(d:ax + by + c = 0\)
a) Từ hình a) ta thấy d đi qua hai điểm\(A(0;2)\) và \(B( - 5;0)\)
\( \Rightarrow \left\{ \begin{array}{l}b.2 + c = 0\\ - 5a + c = 0\end{array} \right. \Rightarrow c = 5a = - 2b\)
Chọn \(a = 2 \Rightarrow b = - 5;c = 10\) và \(d:2x - 5y + 10 = 0\)
Điểm O (0;0) thuộc miền nghiệm và \(2.0 - 5.0 + 10 = 10 > 0\)
Vậy bất phương trình cần tìm là \(2x - 5y + 10 > 0\)
b) Từ hình b) ta thấy d đi qua hai điểm\(A(0;2)\) và \(B(3;0)\)
\( \Rightarrow \left\{ \begin{array}{l}2b + c = 0\\3a + c = 0\end{array} \right. \Rightarrow - c = 3a = 2b\)
Chọn \(a = 2 \Rightarrow b = 3;c = - 6\) và \(d:2x + 3y - 6 = 0\)
Điểm O (0;0) không thuộc miền nghiệm và \(2.0 + 3.0 - 6 = - 6 < 0\)
Vậy bất phương trình cần tìm là \(2x + 3y - 6 > 0\)

Tham khảo:
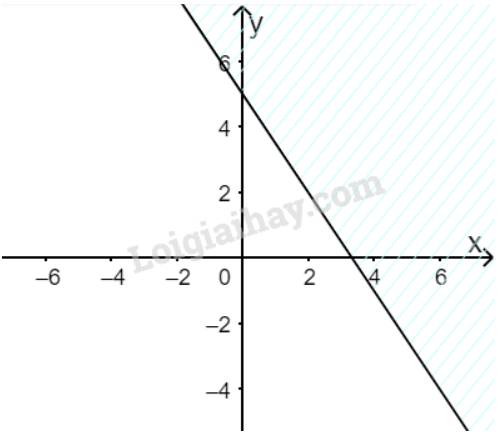
Để pha x lít nước cam loại I cần 30x g bột cam,
Để pha y lít nước cam loại II cần 20y g bột cam,
Vì Cúc chỉ có thể dùng không quá 100 gam bột cam nên ta có bất phương trình \(30x + 20y \le 100\)
\( \Leftrightarrow 3x + 2y - 10 \le 0\)
Vẽ đường thẳng \(\Delta :3x + 2y - 10 = 0\) đi qua hai điểm \(A(0;5)\) và \(B\left( {2;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(3.0 + 2.0 - 10 = - 10 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
 thử ra ngắm nhé
thử ra ngắm nhé
đúng ời
woa vui ghê