Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 5,5 phút=330s
Gọi thời gian người thứ 2 đến nơi là:t(s)
Ta có
S=1,5.(t+330)
S=2.t
=> 1,5(t+330)=2.t
=>t=990(s)
Độ dài quãng đường AB là
2.990=1980(m)

a) Thời gian người thứ hai đến điểm 780m là :
t2 = \(\frac{780}{1,9}\) \(\approx\) 410,5 s
b) 5,50 phút = 300giây + 30giây = 330giây
Gọi t là thời gian người thứ 2 đi => (t+330) là thời gian người thứ nhất đi
Quãng đường người thứ nhất đi: S = 0,9(t+330)
Quãng đường người thứ hai đi: S = 1,9t
=> S = 0,9(t+330) = 1,9t
Ta có phuơng trình: 0,9(t+330)=1,9t; giải hệ có t = 297giây
Vậy vị trí đó cách nơi xuất phát : S =1,9t = 1,9.297 = 564,3m
a) Chọn trục tọa độ trùng với dường thẳng chuyển động , gốc tọa độ là vị trí xuất phát , chiều dương là chiều chuyển động , gốc thời gian là thời điểm xuất phát .
v = \(\frac{\triangle x}{\triangle t}\) → \(\triangle t=\frac{\triangle x}{v}=\frac{780}{1,9}=410,53\left(s\right)=6,84min\) = 6 min 50( s )
b) Gọi t là thời gian người thứ 2 đi cho đến khi dừng lại . Quãng đường người thứ 2 đi được là : S = vt = 1,9t
Cùng trong thời gian t ( s ) , người thứ nhất đi được là : S1 = v1t = 0,9t
Quãng đường người thứ nhất đi được kể từ khi người thứ 2 dừng cho tới lúc gặp nhau là : S2 = v1t` = 0,9 . ( 5,5 . 60 ) 297 ( m )
Ta có : S1 + S2 = S ↔ 297 + 0,9t = 1,9t → t = 297 ( s )
Suy ra : S = 1,9t = 1,9 . 297 = 564,3 ( m )
Vậy vị trí người thứ hai nghỉ cách nơi xuất phát là 564,3 ( m ).

Tổng vận tốc là :
50 : 0,5 = 100 (km/giờ)
Vận tốc xe lớn là :
(100 + 3) : 2 = 51,5 (km/giờ)
Vận tốc xe nhỏ là :
100 - 51,5 = 48,5 (km/giờ)

Câu I:
1. Đặt \(\dfrac{x}{4}=\dfrac{y}{7}=k\)
=> \(\left\{{}\begin{matrix}x=4k\\y=7k\end{matrix}\right.\)
Vì xy = 112 => 4k.7k = 112
=> 28k2 = 112
=> k2 = 4
=> \(\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\)
*) k = 2 => \(\left\{{}\begin{matrix}x=4.2=8\\y=7.2=14\end{matrix}\right.\)
*) k = -2 => \(\left\{{}\begin{matrix}x=4.\left(-2\right)=-8\\y=7.\left(-2\right)=-14\end{matrix}\right.\)
Vậy các cặp (x; y) thỏa mãn là (8; 14) và (-8; -14)
2. *) \(\dfrac{ab+ac}{2}=\dfrac{ba+bc}{3}\) <=> 3(ab + ac) = 2(ba + bc)
<=> ab + 3ac = 2bc
<=> a(b + 3c) = 2bc (1)
*) \(\dfrac{ab+ac}{2}=\dfrac{ca+cb}{4}\) <=> 2(ab + ac) = ca + cb
<=> 2ab + ac = bc
<=> 2a(2b + c) = 2bc (2)
Từ (1) và (2) => a(b + 3c) = 2a(2b + c)
<=> b + 3c = 4b + 2c (vì a ≠ 0)
<=> c = 3b (3)
Thay c = 3b vào (1) ta có:
a(b + 9b) = 6b2
<=> 10ab = 6b2
<=> 5a = 3b (vì b ≠ 0) (4)
Từ (3) và (4) => 5a = 3b = c
<=> \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{15}\)
Vậy bài toán đã được chứng minh
3. P = |2013 - x| + |2014 - x| = |2013 - x| + |x - 2014| ≥ |2013 - x + x - 2014| = |-1| = 1
Dấu "=" xảy ra <=> (2013 - x)(x - 2014) ≥ 0
<=> (x - 2013)(x - 2014) ≤ 0
mà x - 2014 < x - 2013 => \(\left\{{}\begin{matrix}x-2013\ge0\\x-2014\le0\end{matrix}\right.\) <=> 2013 ≤ x ≤ 2014
Vậy min P = 1 tại 2013 ≤ x ≤ 2014
4. +) Xét c = 1 => a + 3 = 5 => a = 2
=> 23 + 3.22 + 5 = 25 = 5b
=> b = 2 (vì b nguyên dương)
+) Xét c > 1 => 5c > 5 => a + 3 > 5 => a > 2
=> a3 + 3a2 + 5 > 25 => 5b > 25 => b > 2
Ta có: a3 + 3a2 + 5 = 5b
<=> a2(a + 3) + 5 = 5b
<=> a2.5c + 5 = 5b
<=> a2.5c - 1 + 1 = 5b - 1 (1)
Vì b > 2 => b - 1 > 0 => 5b - 1 ⋮ 5
Vì c > 1 => c - 1 > 0 => 5c - 1 ⋮ 5 => 5c - 1 + 1 không chia hết cho 5
Ta có: VT(1) không chia hết cho 5; VP(1) ⋮ 5
=> không tồn tại a, b, c nguyên dương thỏa mãn
Vậy cặp số (a; b; c) thỏa mãn là (2; 2; 1)
Câu II:
1. a) y2 + 4x + 2y - 2x + 1 + 2 = 0
<=> (y2 + 2y + 1) + (4x - 2.2x + 1) = 0
<=> (y + 1)2 + (2x - 1)2 = 0
<=> \(\left\{{}\begin{matrix}\left(y+1\right)^2=0\\\left(2^x-1\right)^2=0\end{matrix}\right.\) (vì (y + 1)2 ≥ 0 ∀ y; (2x - 1)2 ≥ 0 ∀ x)
<=> \(\left\{{}\begin{matrix}y+1=0\\2^x=1\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}y=-1\\x=0\end{matrix}\right.\)
Vậy phương trình có nghiệm (x; y) = (0; -1)
b) \(\dfrac{x^2+4x+6}{x+2}+\dfrac{x^2+16x+72}{x+8}=\dfrac{x^2+8x+20}{x+4}+\dfrac{x^2+12x+42}{x+6}\)
ĐKXĐ: x ≠ -2; -4; -6; -8
pt <=> \(\dfrac{\left(x+2\right)^2+2}{x+2}+\dfrac{\left(x+8\right)^2+8}{x+8}=\dfrac{\left(x+4\right)^2+4}{x+4}+\dfrac{\left(x+6\right)^2+6}{x+6}\)
<=> \(\left(x+2\right)+\left(x+8\right)+\dfrac{2}{x+2}+\dfrac{8}{x+8}=\left(x+4\right)+\left(x+6\right)+\dfrac{4}{x+4}+\dfrac{6}{x+6}\)
<=> \(\dfrac{2}{x+2}+\dfrac{8}{x+8}=\dfrac{4}{x+4}+\dfrac{6}{x+6}\)
<=> \(\left(\dfrac{2}{x+2}-1\right)+\left(\dfrac{8}{x+8}-1\right)=\left(\dfrac{4}{x+4}-1\right)+\left(\dfrac{6}{x+6}-1\right)\)
<=> \(\dfrac{-x}{x+2}+\dfrac{-x}{x+8}=\dfrac{-x}{x+4}+\dfrac{-x}{x+6}\)
Nhận xét: x = 0 là một nghiệm của phương trình
Xét x ≠ 0. Chia cả 2 vế cho -x ta có:
\(\dfrac{1}{x+2}+\dfrac{1}{x+8}=\dfrac{1}{x+4}+\dfrac{1}{x+6}\)
<=> \(\dfrac{2\left(x+5\right)}{\left(x+2\right)\left(x+8\right)}=\dfrac{2\left(x+5\right)}{\left(x+4\right)\left(x+6\right)}\)
Nhận xét: x = -5 là một nghiệm của phương trình
Xét x ≠ -5. Chia cả 2 vế cho 2(x + 5) ta có:
\(\dfrac{1}{x^2+10x+16}=\dfrac{1}{x^2+10x+24}\)
<=> x2 + 10x + 16 = x2 + 10x + 24
<=> -8 = 0 (vô lý)
Vậy phương trình có tập nghiệm S = {0; -5}
2. a) A xác định <=> \(\left\{{}\begin{matrix}2x^2+8\ne0\\8-4x+2x^2-x^3\ne0\\x\ne0\\x^2\ne0\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}x\ne0\\x\ne2\end{matrix}\right.\)
\(A=\left(\dfrac{x^2-2x}{2x^2+8}-\dfrac{2x^2}{8-4x+2x^2-x^3}\right)\left(1-\dfrac{1}{x}-\dfrac{2}{x^2}\right)\)

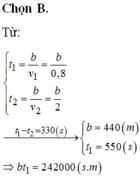
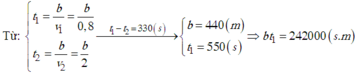
câu b