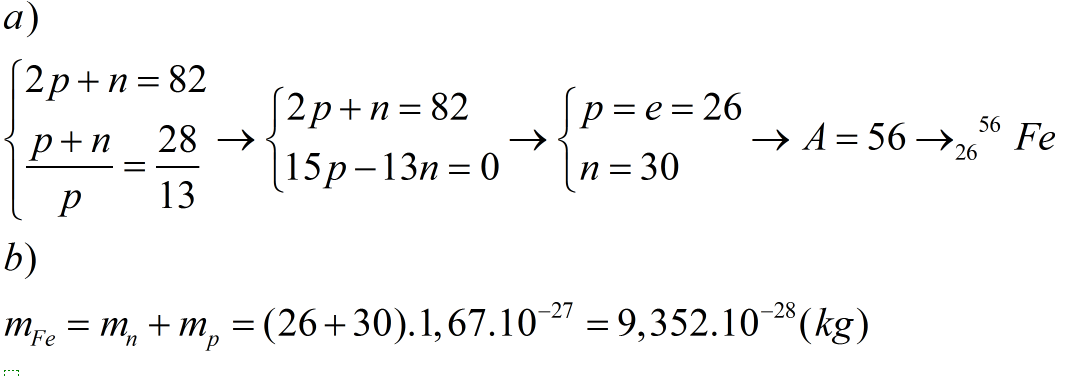Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong ngyên tử A có: số p = số e = Z
số n = N
Theo đề bài ta có: 2Z + N = 122
<=> N = 122 - 2Z (1)
Mặt khác: \(1\le\frac{N}{Z}\le1,5\) (2)
Từ (1) và (2) ta có: \(1\le\frac{122-2Z}{Z}\le1,5\)
<=> \(1\le\frac{122}{Z}-2\le1,5\)
<=> \(3\le\frac{122}{Z}\le3,5\)
<=> \(\frac{244}{7}\le Z\le\frac{122}{3}\)
Mà Z là số nguyên dương
=> Z ∈ {35; 36; 37; 38; 39; 40}
TH1: Z = 35 => N = 52 => A = 87 (loại)
TH2: Z = 36 => N = 50 => A = 86 (loại)
TH3: Z = 37 => N = 48 => A = 85 (nhận)
TH4: Z = 38 => N = 46 => A = 84 (loại)
TH5: Z = 39 => N = 44 => A = 83 (loại)
TH6: Z = 40 => N = 42 => A = 82 (loại)
Vậy nguyên tố A là Rb có Z = 37, N = 85

Z = số proton = số electron. N = số nơtron
Theo đề bài ta có : 2Z + N = 34
Ta biết rằng trong hạt nhân, số nơtron bao giờ cũng bằng hoặc lớn hơn số proton (trừ trường hợp duy nhất là hiđro có Z = 1).
N > Z. Vì vậy ta có : 3Z < 34, do đó Z < 34/3 = 11,3 (1)
Cũng vì N ≥ Z nên theo điều kiện của đề bài Z < 20, do đó :
N/Z ≤ 1,2 → N ≤ 1,2Z
Từ đó ta có : 2Z + N < 2Z + 1,2Z
34 < 3,2 => Z > 34/3,2 = 10,6 (2)
Tổ hợp (1) và (2) ta có : 10,6 < Z < 11,3 mà Z nguyên. Vậy Z = 11. Đó là nguyên tố natri có 11 proton, 11 electron, 12 nơtron.
Số khối của nguyên tử : A = Z + N = 23 => NTK là 23

anh làm chi tiết câu 2 thôi nhé, tại vì dài quá
2.
Ta có: \(\left\{{}\begin{matrix}p+e+n=92\\p=e\\p+e-n=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n=68\\p=e\\p+e+n=92\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=34\\p=e=z=29\end{matrix}\right.\)
\(\Rightarrow A=z+n=29+34=63\left(u\right)\)
\(KHNT:^{63}_{29}Cu\)
3.
Ta có: \(\left\{{}\begin{matrix}p+e+n=155\\p=e\\p+e-n=33\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=z=47\\n=61\end{matrix}\right.\)
\(\Rightarrow A=z+n=47+61=108\left(u\right)\)
\(KHNT:^{108}_{47}Ag\)
4.
Ta có: \(\left\{{}\begin{matrix}p+e+n=58\\p=e\\p+e-n=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=z=19\\n=20\end{matrix}\right.\)
\(\Rightarrow A=z+n=19+20=39\left(u\right)\)
\(KHNT:^{39}_{19}K\)
5.
Ta có: \(\left\{{}\begin{matrix}p+e+n=115\\p=e\\p+e-n=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=z=35\\n=45\end{matrix}\right.\)
\(\Rightarrow A=z+n=35+45=80\left(u\right)\)
\(KHNT:^{80}_{35}Br\)
6.
Ta có: \(\left\{{}\begin{matrix}p+e+n=40\\p=e\\p+e-n=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=z=13\\n=14\end{matrix}\right.\)
\(\Rightarrow A=z+n=13+14=27\left(u\right)\)
\(KHNT:^{27}_{13}Al\)
7.
Ta có: \(\left\{{}\begin{matrix}p+e+n=82\\p=e\\p+e-n=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=z=26\\n=30\end{matrix}\right.\)
\(\Rightarrow A=z+n=26+30=56\left(u\right)\)
\(KHNT:^{56}_{26}Fe\)
8.
Ta có: \(\left\{{}\begin{matrix}p+e+n=40\\p=e\\n-p=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=z=13\\n=14\end{matrix}\right.\)
\(\Rightarrow A=z+n=13+14=27\left(u\right)\)
\(KHNT:^{27}_{13}Al\)
9.
Ta có: \(\left\{{}\begin{matrix}p+e+n=108\\p=e\\n-p=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=z=33\\n=42\end{matrix}\right.\)
\(\Rightarrow A=z+n=33+42=75\left(u\right)\)
\(KHNT:^{75}_{33}As\)
10.
Ta có: \(\left\{{}\begin{matrix}p+e+n=34\\p=e\\n-e=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=z=11\\n=12\end{matrix}\right.\)
\(\Rightarrow A=z+n=11+12=23\left(u\right)\)
\(KHNT:^{23}_{11}Na\)

Theo đề có hệ phương trình:
\(\left\{{}\begin{matrix}2p+n=82\\2p-n=22\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}p=e=26\\n=30\end{matrix}\right.\)
Z: 26
Kí hiệu nguyên tử của nguyên tố X: Fe
b. Đề khác rồi=)

Ta có: \(1\le\dfrac{N}{Z}\le1,5\)
\(\Rightarrow Z\le N\le1,5Z\)
\(\Rightarrow3Z\le2Z+N\le3,5Z\)
Vậy ta có : \(3Z\le24\le3,5Z\)
=> \(6,86\le Z\le8\)
=>\(\left[{}\begin{matrix}Z=7\left(N\right)\\Z=8\left(O\right)\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}N=10\\N=8\end{matrix}\right.\)
Mà theo đề bài : \(1\le\dfrac{N}{Z}\le1,5\)
=> Chỉ có O thỏa mãn
=> Z là O , số P= số E =8 , N=8
b) Cấu hình E: 1s22s22p4