Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2:
ĐK: $m\not\in (-1;+\infty)$
$y=\frac{mx+4}{x+m}\Rightarrow y'=\frac{m^2-4}{(x+m)^2}$
Để $y$ nghịch biến trên khoảng $(-\infty; 1)$ thì:
\(\left\{\begin{matrix} m\not\in (-1;+\infty)\\ y'=\frac{m^2-4}{(x+m)^2}\leq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\not\in (-1;+\infty)\\ -2\leq m\leq 2\end{matrix}\right.\)
Với $m$ nguyên ta suy ra $m=-1; -2$. Vậy có 2 giá trị nguyên của $m$ thỏa mãn.
Câu 1:
Để $y$ đồng biến trên $(-\infty; +\infty)$ thì:
$y'=3x^2-2(2m-1)x+(2-m)\geq 0$ với mọi $x\in\mathbb{R}$
Điều này xảy ra khi: $\Delta'=(2m-1)^2-3(2-m)\leq 0$
$\Leftrightarrow 4m^2-m-5\leq 0$
$\Leftrightarrow (4m-5)(m+1)\leq 0$
$\Leftrightarrow -1\leq m\leq \frac{5}{4}$

y'=2x2-2(2m-3)x+2(m2-3m)=2(x-m)(x-m+3) => h/s nghịch biến trên (m-3; m) => YCBT <=> m-3 =<1 và 3=<m <=> 3=<m=<4

đáp án:
Hàm số đã cho xác định trên D = R.
Với m = -1. Khi đó hàm số trở thành y = -2x + 4 ; y' = -2 < 0 ∀x∈R, không thỏa mãn yêu cầu bài toán.
Với m ≠ -1. Ta có f'(x)= 3(m+1)x2 - 6(m + 1)x + 2m
+ Hàm số đồng biến trên khoảng có độ dài không nhỏ hơn 1 khi và chỉ khi f'(x) = 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn [x1;x2 ] thỏa mãn |x1 - x2 | ≥ 1
+ f'(x)= 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn[x1;x2]
Theo Viét ta có
+ Với |x1 - x2 | ≥ 1 ⇔ (x1 + x2 )2 - 4x1 x2 - 1 ≥ 0
Đối chiếu điều kiện ta có m ≤ -9.

Lời giải:
Đặt \(x^2=t\). Khi đó: \(y=m^2t^2-2(4m-1)t+1\)
\(\Rightarrow y'=2m^2t-2(4m-1)\)
Hàm số ban đầu đồng biến trên \((1;+\infty)\) khi :
\(2m^2t-2(4m-1)\geq 0(*), \forall t\in (1;+\infty)\)
Với \(m=0\Rightarrow (*)\) luôn đúng (thỏa mãn)
Với \(m\geq 0; (*)\Leftrightarrow t\geq \frac{4m-1}{m^2}\) với mọi \(t\in (1;+\infty)\)
\(\Rightarrow \frac{4m-1}{m^2}\leq \min t\Rightarrow \frac{4m-1}{m^2}\leq 1\)
\(\Rightarrow 4m-1\leq m^2\Rightarrow \left[\begin{matrix} m\leq 2-\sqrt{3}\\ m\geq 2+\sqrt{3}\end{matrix}\right.\)
Vậy \(m\in (-\infty; 2-\sqrt{3}]; m\in [2+\sqrt{3}; +\infty)\)
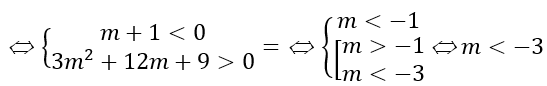
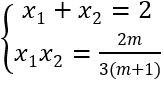
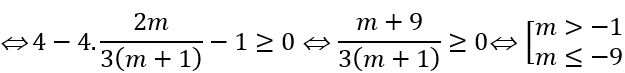
Chọn C