K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

16 tháng 2 2017
Lời giải:
Giả sử tồn tại các số nguyên a,b,c,d thỏa bài toán
Ta có abcd − a = a(bcd − 1) = 1357 là số lẻ nên a là số lẻ
Tương tự b,c,d cũng là số lẻ
Như vậy abcd lẻ và a lẻ suy ra abcd − a là số chẵn (vô lý)
Vậy không tồn tại các số nguyên a, b, c, d thỏa bài toán

CM
16 tháng 1 2019
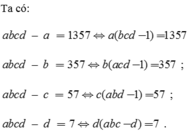
Nếu 1 trong a,b,c,d chẵn thì 1 trong 4 đẳng thức sai (kết quả ra chẵn do 1 số chẵn nhân 1 tích thì chẵn) =>a,b,c,d không tồn tại (do a,b,c,d phải thoả cả 4 đẳng thức)
Nếu a,b,c,d đều lẻ thì 1số lẻ nhân cho 1 số chẵn (tích 3 số lẻ trừ 1 thì chẵn) thì là một số chẵn=>a,b,c,d không tồn tại
Vậy không tồn tại các số nguyên a,b,c,d để thoả yêu cầu đề bài
NQ
4


Đáp án:
Giải thích các bước giải:
Không tồn tại số a,b,c,d
Vì ta có abcd là số có 4 chữ số
abcd-d=7
Số có 4 chữ số - số đơn vị=7( vô lí)
=> không tồn tại a,b,c,d
học tốt
vì abcd là sn có 4 c/s
=> abcd=a000+b00+c0+d
có abcd-d =abc0
=> chữ số cuối cùng của abcd phải là 0 mâu thuẫn với abcd-d=7
=> không tồn tại 4 chữ số nguyên a;b;c;d cần tìm