DT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
2
NT
3
NM
10 tháng 9 2019
342+662+68.66
=342+68.66+662
=342+2.34.66+662
=(34+66)2=1002
=10000
HH
26 tháng 2 2020
A B C K H I
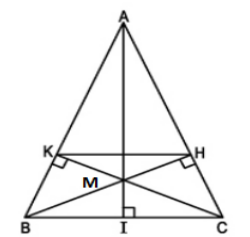
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)
NY
0
HH
2
3 tháng 9 2017
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó ΔBDE cân. b) Ta có AC // BE suy ra
= 
(3)
∆BDE cân tại B (câu a) nên 
= (4)
Từ (3) và (4) suy ra =
Xét ∆ACD và ∆BCD có AC = BD (gt)
= (cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (cmt - câu b)
=> Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
P/S : Mình lười vẽ hình nên chỉ mướn trên mạng nha!3 tháng 9 2017
a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BÉ song song nên chúng bằng nhau:
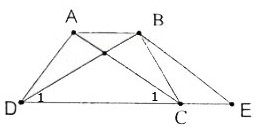
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE \(\Rightarrow\widehat{C}_1=\widehat{E}\) (3)
∆BDE cân tại B (câu a) nên \(\Rightarrow\widehat{D_1}=\widehat{E}\) (4)
Từ (3) và (4) \(\Rightarrow\widehat{C_1}=\widehat{D_1}\)
Xét ∆ACD và ∆BCD có
AC = BD (gt)
\(\widehat{C_1}=\widehat{D_1}\) (cmt)
CD cạnh chung
\(\Rightarrow\) ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
\(\Rightarrow\widehat{ADC}=\widehat{BCD}\)
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
26 tháng 5 2020
2, \(\widehat{ABC} + \widehat{BCA} = \widehat{BAC} = 90^0 ⇒ \widehat{BCA} = 90^0 - \widehat{ABC}\)
\(\widehat{ABC} +\widehat{ BAH} = \widehat{BAC} =90^0⇒\widehat{BAH} = 90^0 - \widehat{ABC}\)
\(\widehat{BCA} = \widehat{BAH}\)
XÉT \(\bigtriangleup\)HBA và\(\bigtriangleup\) HAC có :
\(\widehat{BHA}=\widehat{BAC}=90^0\)
\(\widehat{BCA}=\widehat{BAH}\)
⇒ \(\bigtriangleup\)HBA ∼ \(\bigtriangleup\) HAC
b, Áp dụng hệ thức \(b^2=a.b'\) vào \(\bigtriangleup{ABC}\) vuông tại A , ta có :
\(AC^2=BC.CH\) (đpcm)
c, Áp dụng hệ thức \(h^2=b'.c'\) vào \(\bigtriangleup{ABC}\) vuông tại A, ta có :
\(AH^2=BH.CH\) (đpcm)
8 tháng 10 2019
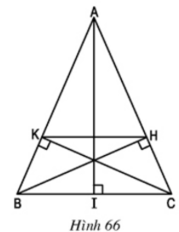
Bài 64 (trang 100 SGK Toán 8 Tập 1): Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
8 tháng 10 2019
Theo giả thiết ABCD là hình bình hành nên ta có:
ˆDAB=ˆDCB,ˆADC=ˆABC (1)
Theo định lí tổng các góc của một tứ giác ta có:
ˆDAB+ˆDCB+ˆADC+ˆABC=360o (2)
Từ (1) và (2) ⇒ˆDAB+ˆABC=360o/2=180o
Vì AG là tia phân giác ˆDAB (giả thiết)
⇒⇒ ˆBAG=1/2ˆDAB (tính chất tia phân giác)
Vì BG là tia phân giác ˆABC (giả thiết)
⇒⇒ ˆABG=1/2ˆABC
Do đó: ˆBAG+ˆABG=1/2(ˆDAB+ˆABC)=1/2.1800=90o
Xét ΔAGB= có:
ˆBAG+ˆABG=90o (3)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác AGBAGB ta có:
ˆBAG+ˆABG+ˆAGB=180o (4)
Từ (3) và (4) ⇒ˆAGB=90o
Chứng minh tương tự ta được: ˆDEC=ˆEHG=90o
Tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
G
20 tháng 9 2017
Bài giải: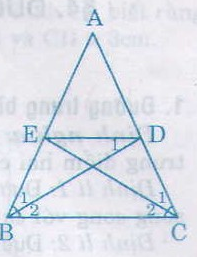 
a) ∆ABD và ∆ACE có
AB = AC (gt)
\(\widehat{A}\) chung
\(\widehat{B_1}=\widehat{C_1}\left(=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}\widehat{C}\right)\)
Nên ∆ABD = ∆ACE (g.c.g)
Suy ra AD = AE
Chứng minh BEDC là hình thang cân như câu a của bài 15.
b) Vì BEDC là hình thang cân nên DE // BC.
Suy ra \(\widehat{D_1}=\widehat{B_2}\) (so le trong)
Lại có \(\widehat{B_2}=\widehat{B_1}\) nên \(\widehat{B_1}=\widehat{D_1}\)
Do đó tam giác EBD cân. Suy ra EB = ED.
Vậy BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Chúc bạn học tốt!
31. a) \(\left(a+b\right)^3-3ab\left(a+b\right)\)
\(=a^3+3a^2b+3ab^2+b^3-3a^2b+3ab^2\)
\(=a^3+b^3\)
b) \(\left(a-b\right)^3+3ab\left(a-b\right)\)
\(=a^3-3a^2b+3ab^2-b^3+3a^2b-3ab^2\)
\(=a^3-b^3\)
Áp dụng: \(a^3+b^3\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)\)
\(=-125+90\)
\(=-35\)
35. a) \(34^2+66^2+68.66\)
\(=34^2+2.34.66+66^2\)
\(=\left(34+66\right)^2=100^2=10000\)
b) \(74^2+24^2-48.74\)
\(=74^2-2.74.24+24^2\)
\(=\left(74-24\right)^2=50^2=2500\)
Nhớ tick
Bạn ghi hẳn đề lên nhé