
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : \(a^3=10+3\sqrt[3]{\left(5+\sqrt{52}\right)\left(5-\sqrt{52}\right)}\left(\sqrt[3]{5+\sqrt{52}}+\sqrt[3]{5-\sqrt{52}}\right)\)
\(=10+3\sqrt[3]{-27}.a=10-9a\)
\(\Rightarrow a^3+9a-10=0\Rightarrow\left(a-1\right)\left(a^2+a+10\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}a-1=0\\a^2+a+10=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}a=1\\\left(a+\dfrac{1}{2}\right)^2+\dfrac{39}{4}>0\end{matrix}\right.\)
\(\Rightarrow a=1\) \(\Rightarrow f\left(a\right)=1+1+1^2+.....+1^{2015}=2016\)

1. ĐKXĐ: $x\in\mathbb{R}$
PT $\Leftrightarrow 4x=\sqrt{(3x+1)^2}$
\(\Leftrightarrow \left\{\begin{matrix} x\geq 0\\ (4x)^2=(3x+1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 0\\ (4x-3x-1)(4x+3x+1)=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq 0\\ (x-1)(7x+1)=0\end{matrix}\right.\Leftrightarrow x=1\)
Vậy $x=1$ là nghiệm của pt.
2. ĐKXĐ: $x\geq -5$
PT $\Leftrightarrow \sqrt{4}.\sqrt{x+5}-3\sqrt{5+x}+\frac{4}{3}.\sqrt{9}.\sqrt{x+5}=0$
$\Leftrightarrow 2\sqrt{x+5}-3\sqrt{x+5}+4\sqrt{x+5}=0$
$\Leftrightarrow 3\sqrt{x+5}=0$
$\Leftrightarrow \sqrt{x+5}=0$
$\Leftrightarrow x=-5$

Cái này giải căn từ phải qua trái, tức là giải từ căn nhỏ đến căn lớn.
Ngại làm quá =))). Thôi làm cho 1 ý bạn tự suy ra nhé.
\(a.\sqrt{6+2\sqrt{5-\sqrt{13+\sqrt{48}}}}\)
\(=\sqrt{6+2\sqrt{5-\sqrt{12+2.\sqrt{12}.1+1}}}\)
\(=\sqrt{6+2\sqrt{5-\left|\sqrt{12}+1\right|}}\)
\(=\sqrt{6+2\sqrt{5-\sqrt{12}-1}}\)
\(=\sqrt{6+2\sqrt{4-\sqrt{12}}}\)
\(=\sqrt{6+2\left|\sqrt{3}-1\right|}\)
\(=\sqrt{6+2\sqrt{3}-2}\)
\(=\sqrt{2\sqrt{3}+4}\)
\(=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)
a)\(\sqrt{6+2\sqrt{5-\sqrt{1+12+4\sqrt{3}}}}=\sqrt{6+2\sqrt{5-1-2\sqrt{3}}}=\sqrt{6+2\sqrt{3}-2}=\sqrt{1+3+2\sqrt{3}}=1+\sqrt{3}\)
b)\(\sqrt{\sqrt{5}-\sqrt{3-\sqrt{20+9-4\sqrt{5}}}}=\sqrt{\sqrt{5}-\sqrt{3-2\sqrt{5}+3}}\)
=\(\sqrt{\sqrt{5}-\sqrt{5+1-2\sqrt{5}}}=\sqrt{\sqrt{5}-\sqrt{5}+1}=\sqrt{1}=1\)
mk chỉ biết làm đến đấy thôi

Lời giải:
1)
Để biểu thức có nghĩa thì:
\(2x^2-5x+3\geq 0\)
\(\Leftrightarrow 2x(x-1)-3(x-1)\geq 0\)
\(\Leftrightarrow (2x-3)(x-1)\geq 0\)
\(\Leftrightarrow \left[\begin{matrix} x\geq \frac{3}{2}\\ x\leq 1\end{matrix}\right.\)
2)
\(\sqrt{6.5+\sqrt{12}}+\sqrt{6.5-\sqrt{12}}+2\sqrt{6}\)
\(=\sqrt{(\sqrt{6})^2+(\frac{1}{\sqrt{2}})^2+2\sqrt{6}.\frac{1}{\sqrt{2}}}+\sqrt{(\sqrt{6})^2+(\frac{1}{\sqrt{2}})^2-2\sqrt{6}.\frac{1}{\sqrt{2}}}+2\sqrt{6}\)
\(=\sqrt{(\sqrt{6}+\frac{1}{\sqrt{2}})^2}+\sqrt{(\sqrt{6}-\frac{1}{\sqrt{2}})^2}+2\sqrt{6}\)
\(=\sqrt{6}+\frac{1}{\sqrt{2}}+\sqrt{6}-\frac{1}{\sqrt{2}}+2\sqrt{6}=4\sqrt{6}\)

TA CÓ:
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1+6\sqrt{x-1}+9}=5\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(\sqrt{x-1}-3\right)^2}=5\)
\(\Leftrightarrow\sqrt{x-1}-2+\sqrt{x-1}-3=5\Leftrightarrow2\sqrt{x-1}=10\Leftrightarrow\sqrt{x-1}=5\)
\(\Leftrightarrow x-1=25\Leftrightarrow x=26\)
ĐKXĐ: \(x\ge1\)
PT (=) \(\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(\sqrt{x-1}+3\right)^2}=5\)
(=) \(\sqrt{x-1}-2+\sqrt{x-1}+3=5\) (=) \(2\sqrt{x-1}=4\)(=) \(\sqrt{x-1}=2\)(=) X = 5 (nhận)

@Nguyễn Thị Thu Sương :
\(\frac{\sqrt{3+\sqrt{15}}}{\sqrt{2}}=\sqrt{\frac{3+\sqrt{15}}{2}}\)
\(=\sqrt{\frac{\sqrt{3}\left(\sqrt{3}+\sqrt{5}\right)}{5-3}}\)
\(=\sqrt{\frac{\sqrt{3}\left(\sqrt{3}+\sqrt{5}\right)}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}}\)
\(=\sqrt{\frac{\sqrt{3}}{\sqrt{5}-\sqrt{3}}}\)
a) \(\left(\sqrt{12}-\sqrt{27}+\sqrt{3}\right):\sqrt{3}\)
\(=\left(2\sqrt{3}-3\sqrt{3}+\sqrt{3}\right):\sqrt{3}\)
\(=\sqrt{3}\left(2-3+1\right):\sqrt{3}\)
\(=0:\sqrt{3}=0\)
b) \(\left(5\sqrt{3}+3\sqrt{5}\right):\sqrt{15}\)
\(=\frac{5\sqrt{3}}{\sqrt{15}}+\frac{3\sqrt{5}}{\sqrt{15}}\)
\(=\frac{5\sqrt{3}}{\sqrt{3}\cdot\sqrt{5}}+\frac{3\sqrt{5}}{\sqrt{3}\cdot\sqrt{5}}\)
\(=\sqrt{5}+\sqrt{3}\)
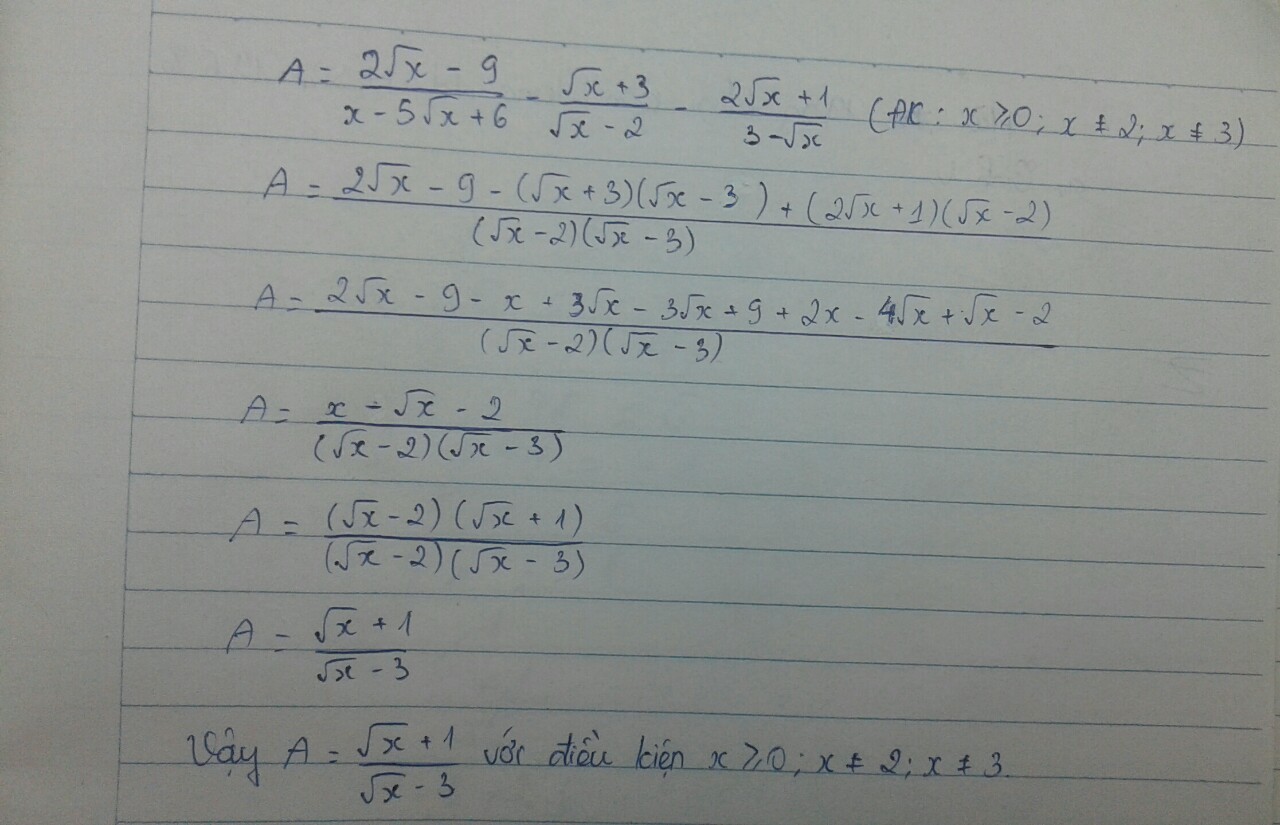 mình trình bày trong hình, hơi mờ bạn thông cảm!
mình trình bày trong hình, hơi mờ bạn thông cảm!
\(x=\sqrt{6+\sqrt{20}}\)
\(\rightarrow x=\sqrt{6+2\sqrt{5}}\)
\(\rightarrow x=\sqrt{5+2\sqrt{5}+1}\)
\(\rightarrow x=\sqrt{\left(\sqrt{5}\right)^2+2\sqrt{5}+1^2}\)
\(\rightarrow x=\left|\sqrt{5}+1\right|\)
\(\rightarrow x=\sqrt{5}+1\)
gần = 3,23606797749979