Tính và so sánh: 2 . 5 2 v à 2...

Tính và so sánh: 2 . 5...

LH

Luyện Hoàng Khánh Linh

11 tháng 11 2016 - olm

Câu 1: Chứng minh:

\(31.82+125.48+21.43=125.67=1500\)

Câu 2: So sánh:

1,\(\sqrt{51}-\sqrt{5}v\text{à}\sqrt{20}-\sqrt{6}\)

2,\(\sqrt{2}+\sqrt{8}v\text{à}\sqrt{3}+3\)

3,\(\sqrt{37}-\sqrt{14}v\text{à}6-\sqrt{15}\)

4,\(\sqrt{5}+\sqrt{10}v\text{à}5,3\)

#Hỏi cộng đồng OLM #Toán lớp 7

0

NT

Nguyễn Thị MInh Huyề

27 tháng 6 2019 - olm

So sánh :

\(a,2^{30}v\text{à}3^{20}\)

\(b,5^{300}v\text{à}3^{500}\)

\(c,2^{24}v\text{à}3^{16}\)

\(d,\left(0,3\right)^{40}v\text{à}\left(0,1\right)^{20}\)

#Hỏi cộng đồng OLM #Toán lớp 7

5

MH

Mathematics♡ ح ح ℌ ♡Physical

27 tháng 6 2019

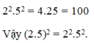
\(\text{a, }2^{30}=8^{10}\)

\(\text{ }3^{20}=\left(3^2\right)^{10}=9^{10}\)

\(\text{Vậy }2^{30}< 3^{20}\)

Đúng(0)

MH

Mathematics♡ ح ح ℌ ♡Physical

27 tháng 6 2019

\(\text{b, }5^{300}=\left(5^3\right)^{100}=125^{100}\)

\(3^{500}=\left(3^5\right)^{100}=243^{100}\)

\(\text{Vậy }5^{300}< 243^{100}\)

Đúng(0)

HN

Hoàng Nguyễn Công

28 tháng 3 2019 - olm

So sánh:

\(\left(-\frac{1}{5}\right)^{255}v\text{à}\left(-\frac{1}{2}\right)^{579}\)

#Hỏi cộng đồng OLM #Toán lớp 7

0

NT

Nguyễn Thị MInh Huyề

27 tháng 6 2019 - olm

So sánh

\(a,2^{30}+3^{30}+4^{30}v\text{à}3^{20}+6^{20}+8^{20}\)

\(b,2^{30}+3^{30}+4^{30}v\text{à}3.24^{10}\)

\(c,2^0+2^1+2^2+...+2^{50}v\text{à}2^{51}\)

#Hỏi cộng đồng OLM #Toán lớp 7

3

KN

Kiệt Nguyễn

28 tháng 6 2019

c) Đặt \(A=2^0+2^1+2^2+...+2^{50}\)

\(\Leftrightarrow2A=2^1+2^2+2^3...+2^{51}\)

\(\Leftrightarrow2A-A=2^1+2^2+2^3...+2^{51}\)\(-2^0-2^1-2^2-...-2^{50}\)

\(\Leftrightarrow A=2^{51}-2^0=2^{51}-1< 2^{51}\)

Vậy \(2^0+2^1+2^2+...+2^{50}< 2^{51}\)

Đúng(1)

KN

Kiệt Nguyễn

28 tháng 6 2019

a)Ta có: \(\hept{\begin{cases}2^{30}=\left(2^3\right)^{10}=8^{10}\\3^{30}=\left(3^3\right)^{10}=27^{10}\\4^{30}=\left(2^2\right)^{30}=2^{60}\end{cases}}\)và \(\hept{\begin{cases}3^{20}=\left(3^2\right)^{10}=9^{10}\\6^{20}=\left(6^2\right)^{10}=36^{10}\\8^{20}=\left(2^3\right)^{20}=2^{60}\end{cases}}\)

Mà \(8^{10}< 9^{10}\); \(27^{10}< 36^{10}\);\(2^{60}=2^{60}\)nên

\(8^{10}+27^{10}+2^{60}< 9^{10}+36^{10}+2^{60}\)

hay \(2^{30}+3^{30}+4^{30}< 3^{20}+6^{20}+8^{20}\)

Đúng(0)

S

sannnnna

21 tháng 6 2018 - olm

1. so sánh

\(2^{27}v\text{à}3^{18}\)

\(3^{21}v\text{à}2^{31}\)

#Hỏi cộng đồng OLM #Toán lớp 7

2

A

Anna

21 tháng 6 2018

\(2^{27}=2^{3.9}=8^9\)

\(3^{18}=3^{2.9}=9^9\)

Vì \(9^9>8^9\Rightarrow3^{18}>2^{27}\)

Đúng(0)

LT

Lưu Thiên Hương

21 tháng 6 2018

MK chỉ làm đc câu a) thui nha :

2^27 = 2^ 3.9 = 8^9

3^18 = 3^2.9=9^9

Vì 9^9 > 8^9 => 2^27 < 2 ^18

Đúng(0)

NT

Nguyễn Thuỳ Linh

24 tháng 2 2020 - olm

So sánh:

a)\(2^{24}v\text{à}3^{16}\)

b)\(2^{300}v\text{à}3^{200}\)

c)\(71^5v\text{à}7^{20}\)

#Hỏi cộng đồng OLM #Toán lớp 7

2

YN

Yêu nè

24 tháng 2 2020

a) Ta có \(\hept{\begin{cases}2^{24}=\left(2^6\right)^4=64^4\\3^{16}=\left(3^4\right)^4=81^4\end{cases}}\)

Mà \(64< 81\)

\(\Rightarrow64^4< 81^4\)

\(\Rightarrow2^{24}< 3^{16}\)

b) Ta có \(\hept{\begin{cases}2^{300}=\left(2^3\right)^{100}=8^{100}\\3^{200}=\left(3^2\right)^{100}=9^{100}\end{cases}}\)

Mà 8 < 9

\(\Rightarrow8^{100}< 9^{100}\)

\(\Rightarrow2^{300}< 3^{200}\)

c) Ta có \(7^{20}=\left(7^4\right)^5=2401^5\)

Ta có 71 < 2401

\(\Rightarrow71^5< 2401^5\)

\(\Rightarrow71^5< 7^{20}\)

!! K chắc câu c

@@ Học tốt

Chiyuki Fujito

Đúng(0)

TL

Tran Le Khanh Linh

24 tháng 2 2020

a) \(2^{24}=\left(2^3\right)^8=8^8\)

\(3^{16}=\left(3^2\right)^8=9^8\)

Ta thấy 8<9\(\Rightarrow8^8< 9^8\Rightarrow2^{24}< 3^{16}\)

b) \(2^{300}=\left(2^3\right)^{100}=8^{100}\)

\(3^{200}=\left(3^2\right)^{100}=9^{100}\)

Thấy \(8< 9\Rightarrow8^{100}< 9^{100}\Rightarrow2^{300}< 3^{200}\)

c) \(7^{20}=\left(7^4\right)^5=2401^5\)

Ta thấy \(71< 2401\Rightarrow71^5< 2401^5\Rightarrow71^5< 7^{20}\)

Đúng(0)

HT

Hoàng Thị Quỳnh Trâm

22 tháng 7 2021 - olm

1. Tính

\(\frac{8^{10}+4^{10}}{8^4+4^{11}}\)

2.So sánh

\(2^{24}v\text{à}3^{16}\) \(2^{150}v\text{à}3^{100}\)

mọi ng giúp mk với nhé, mk đang cần rất gấp!!!

#Hỏi cộng đồng OLM #Toán lớp 7

0

NN

Ngu Người

25 tháng 10 2015 - olm

so sánh \(\frac{1}{101^2}+\frac{1}{102^2}+...+\frac{1}{205^2}v\text{à}\frac{1}{2^2\cdot3\cdot5^2\cdot7}\)

#Hỏi cộng đồng OLM #Toán lớp 7

2

HT

Hồ Thu Giang

25 tháng 10 2015

Đặt A = \(\frac{1}{101^2}+\frac{1}{102^2}+...+\frac{1}{205^2}\)

=> A < \(\frac{1}{100.101}+\frac{1}{101.102}+....+\frac{1}{204.205}\)

=> A < \(\frac{1}{100}-\frac{1}{101}+\frac{1}{101}-\frac{1}{102}+...+\frac{1}{204}-\frac{1}{205}\)

=> A < \(\frac{1}{100}-\frac{1}{205}\)

=> A < \(\frac{1}{2100}\)

Đặt B = \(\frac{1}{2^2.3.5^2.7}=\frac{1}{2100}\)

=> A < B

=> \(\frac{1}{101^2}+\frac{1}{102^2}+...+\frac{1}{205^2}<\frac{1}{2^2.3.5^2.7}\)

Đúng(0)

NN

Ngu Người

25 tháng 10 2015

giỏi lắm mình cũng biết làm chỉ hỏi chơi thôi

ủng hộ

Đúng(0)

LN

le ngoc anh

7 tháng 1 2018

so sánh

a, \(\sqrt{2}+\sqrt{3}+\sqrt{5}v\text{à}18\)

b, \(\sqrt{5}+\sqrt{7}+4v\text{à}12\)

#Hỏi cộng đồng OLM #Toán lớp 7

3

MS

Mashiro Shiina

7 tháng 1 2018

\(\sqrt{2}+\sqrt{3}+\sqrt{5}< \sqrt{4}+\sqrt{9}+\sqrt{25}=2+3+5=10< 18\)

b) \(\sqrt{5}+\sqrt{7}+4< \sqrt{9}+\sqrt{9}+4=3+3+4=10< 12\)

Đúng(0)

LN

le ngoc anh

7 tháng 1 2018

nhanh hộ mình với

Đúng(0)

VN

Vũ Nga

17 tháng 8 2020 - olm

Bài 1: So sánh \(2^{225}\) và Bài 2: Tìm số nguyên n lớn nhất sao cho \(n^{150}\)< \(5^{225}\)Bài 3: Tính:\(M=2^{2010}-(2^{2009}+2^{2008}+....+2^1+2^0)\)Bài 4: So sánh \(3^{4000}\) và \(9^{2000}\) bằng hai cáchBài 5:So...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

4

TT

Trí Tiên

17 tháng 8 2020

bài 4 : c1 \(3^{4000}\)và \(9^{2000}\)

\(\Leftrightarrow9^{2000}\Leftrightarrow\left(3^2\right)^2^{000}\Leftrightarrow3^{4000}\)

vì \(3^{4000}=3^{4000}\Leftrightarrow3^{4000}=9^{2000}\)

c2

ta có

\(3^{4000}=\left(3^4\right)^{1000}=81^{1000}\)

\(9^{2000}=\left(9^2\right)^{1000}=81^{1000}\)

vì \(81^{1000}=81^{1000}\Leftrightarrow3^{4000}=9^{2000}\)

bài 5

\(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)

\(3^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)

vì \(8^{111}< 9^{111}\Leftrightarrow2^{332}< 3^{223}\)

Đúng(0)

XO

Xyz OLM

17 tháng 8 2020

3) M = 2²⁰¹⁰ - (2²⁰⁰⁹ + 2²⁰⁰⁸ + .... + 2¹ + 2⁰)

Đặt N = 2²⁰⁰⁹ + 2²⁰⁰⁸ + .... + 2¹ + 2⁰

=> 2N = 2²⁰¹⁰ + 2²⁰⁰⁹ + .... + 2² + 2¹

=> 2N - N = (2²⁰¹⁰ + 2²⁰⁰⁹ + .... + 2² + 2¹) - (2²⁰⁰⁹ + 2²⁰⁰⁸ + .... + 2¹ + 2⁰)

=> N = 2²⁰¹⁰ - 1

Khi đó M = 2²⁰¹⁰ - (2²⁰¹⁰ - 1) = 1

4) C1 Ta có 3⁴⁰⁰⁰ = (3⁴)¹⁰⁰⁰ = 81¹⁰⁰⁰ = (9²)¹⁰⁰⁰ = 9²⁰⁰⁰

3⁴⁰⁰⁰ = 9²⁰⁰⁰

C2 Ta có : 3⁴⁰⁰⁰ = (3⁴)¹⁰⁰⁰ = 81¹⁰⁰⁰ (1)

Lại có 9²⁰⁰⁰ = (9²)¹⁰⁰⁰ = 81¹⁰⁰⁰ (2)

Từ (1) (2) => 3⁴⁰⁰⁰ = 9²⁰⁰⁰

5 Ta có 2³³² < 2³³³ = (2³)¹¹¹ = 8¹¹¹ < 9¹¹¹ = (3²)¹¹¹ = 3²²² < 3²²³

=> 2³³² < 3²²³

2) Ta có n¹⁵⁰ < 5²²⁵

=> (n⁵)⁷⁵ < (5³)⁷⁵

=> n⁵ < 5³

=> n⁵ < 125

Vì n là số nguyên lớn nhất => n = 2

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP