LX
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 4 2023
#include <bits/stdc++.h>
using namespace std;
int B[100],n,t;
{
cin>>n;
for (int i=1; i<=n; i++) cin>>B[i];
t=0;
for (int i=1; i<=n; i++)
if (B[i]%10==0) t+=B[i];
cout<<t<<endl;
int dem=0;
for (int i=1; i<=n; i++)
if ((i%2==0) && (A[i]%2!=0)) dem++;
cout<<dem<<endl;
for (int i=1; i<=n; i++)
if ((A[i]%2!=0) && (A[i]%3==0)) cout<<A[i];
}
CM
31 tháng 1 2017
Chọn C
Ta có 
Gọi số tự nhiên cần tìm có bốn chữ số là a b c d ¯
Vì a b c d ¯ chia hết cho 11 nên (a + c) - (b + d) ⋮ 11
=> (a + c) - (b + d) = 0 hoặc (a + c) - (b + d) = 11 hoặc (a + c) - (b + d) = -11 do
Theo đề bài ta cũng có a + b + c + d chia hết cho 11
Mà 
hoặc 
Vì 
nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ
(do các trường hợp còn lại không thỏa mãn) => (a,c) và (b,d) là một trong các cặp số:
- Chọn 2 cặp trong số 4 cặp trên ta có C 4 2 cách.
- Ứng với mỗi cách trên có 4 cách chọn a; 1 cách chọn c; 2 cách chọn b; 1 cách chọn d.
Vậy xác suất cần tìm là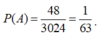 
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Ta có: \({u_n} = 3n,\;\forall n \in {N^*}\).
b) Ta có: \({u_n} = 4n + 1,\forall n \in {N^*}\;\).
.
CM
3 tháng 7 2018
Đáp án B
Phép thử : “ Rút 1 số từ tập S”
=> 
Biến cố A: “ Số có 7 chữ số khác nhau mà các số 3,4,5 liền nhau và cả 6,9 liền nhau”
TH1: Không có mặt chữ số 0
=> Số các số thỏa mãn là: 
TH2: Có mặt chữ số 0
=> Số các số thỏa mãn là: 
Vậy xác suất cần tìm là : 
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 12 2021
Gọi số đó là \(\overline{abcdef}\Rightarrow a+b+c+d+e+f=1+2+3+4+5+6=21\)
Mặt khác \(a+b+c=d+e+f-1\)
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=10\\d+e+f=11\end{matrix}\right.\)
\(\Rightarrow\left(a;b;c\right)=\left(1;3;6\right);\left(1;4;5\right);\left(2;3;5\right)\)
Số số thỏa mãn: \(3.\left(3!.3!\right)=108\)
Xác suất: \(P=\dfrac{108}{6!}=\dfrac{3}{20}\)
TA
7 tháng 10 2022
GỌI E = {3;6}; F = {1;4;7} ; G = {2;5} ; H= {0}
LẬP 4 chữ số ABCD đôi một khác nhau
1: Chứa số 0 trong 3 chữ số B,C,D là 3 cách
Chọn 1 số trong E và F và G thì (E+F+G):3 chia hết (loại)
Chọn 2 số trong E và 1 số trong F thì (E+E+F):3 dư 1 (loại)
-Chọn 1 số trong E và 2 số trong F thì (E+F+F):3 dư 2 (1)
Từ (1) => 3 trong 2 số thuộc F : 3C2 là 3 cách
Và 1 trong 2 số thuộc E : 2C1 là 2 cách
ABCD chứa 0 thì A và 2 chữ số (không chứa 0) sắp xếp 3!
(1) Số lập được 3.3.2.3! = 108 số
-Chọn 2 số trong E và 1 số trong G thì (E+E+G):3 dư 2 (2)
Từ (2) => 2 trong 1 số thuộc G : 2C1 là 2 cách
Và 2 trong 2 số thuộc E : 2C2 là 1 cách
ABCD chứa 0 thì A và 2 chữ số (không chứa 0) sắp xếp 3!
(2) Số lập được 3.2.1.3! = 36 số
Chọn 1 số trong E và 2 số trong G thì (E+G+G):3 dư 1 (loại)
Chọn 2 số trong F và 1 số trong G thì (F+F+G):3 dư 1 (loại)
Chọn 1 số trong F và 2 số trong G thì (F+G+G):3 dư 2 (3)
Từ (3) => 3 trong 1 số thuộc F : 3C1 là 3 cách
Và 2 trong 2 số thuộc G : 2C2 là 1 cách
ABCD chứa 0 thì A và 2 chữ số (không chứa 0) sắp xếp 3!
(3) Số lập được 3.3.1.3! = 54 số
2: Không chứa 0
-Chọn 1 số trong E và F và 2 số trong G: (E+F+G+G):3 dư 2 (4)
Từ (4) => 1 số trong E : 2C1 là 2 cách và trong F : 3C1 là 3 cách
2 số trong G : 2C2 là 1 cách
ABCD thì A,B,C,D sắp xếp 4!
(4) Số lập được 2.3.1.4! = 144 số
Chọn 1 số trong E và G và 2 số trong F: (E+F+F+G):3 dư 1 (loại)
Chọn 2 số trong E và 1 số trong F và G: (E+E+F+G):3 không dư (loaị)
-Chọn 2 số trong E và F: (E+E+F+F):3 dư 2 (5)
Từ (5) => 2 số trong E: 2C2 là 1 cách và trong F: 3C2 là 3 cách
ABCD thì A,B,C,D sắp xếp 4!
(5) Số lập được 1.3.4! = 72 số
Chọn 2 số trong E và G: (E+E+G+G):3 dư 1 (loại)
Vậy từ (1),(2),(3),(4),(5) ta có 108+36+54+144+72 = 414 số
<=> Tổng cộng có 414 số thỏa mãn yêu cầu đề bài.
12 tháng 5 2023
n(S)=6!
Để thỏa mãn yêu cầu đề bài thì cần chọn ra 3 số có tổng là 12
=>Số trường hợp thỏa mãn là (1;5;6); (2;4;6); (3;4;5)
=>Có 3*3!*3!
=>P=3/20
.Số nhỏ nhất chia 5 dư 3 có 3 chữ số là:103.
Số lớn nhất chia 5 dư 3 là:998.
Khoảng cách của mỗi số là 5.
Có số số hạng là:
(998-103):5+1=180
Tổng các số có 3 chữ số chia 5 dư 3 là:
(998+103).180:2=99090
Đáp số:99090.