Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đồ thị như hình bên.
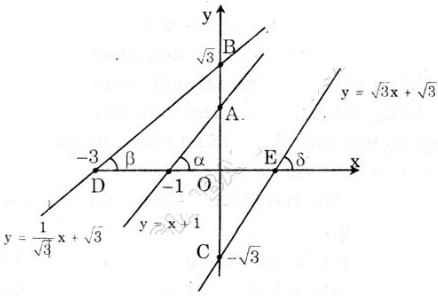
b) tgα = 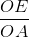 = 1,
= 1,
tgβ = 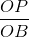 =
= 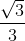 =
= 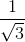 ,
,
tgɣ = 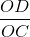 =
= 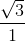 = √3.
= √3.
Suy ra α = 450, β = 300, ɣ = 600 .
a) Đồ thị như hình bên.

b) tgα = 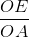 = 1,
= 1,
tgβ = 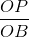 =
= 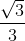 =
= 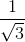 ,
,
tgɣ = 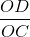 =
= 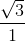 = √3.
= √3.
Suy ra α = 450, β = 300, ɣ = 600 .

a/ \(k=-1=tan\alpha\Rightarrow\alpha=135^0\)
b/ Phương trình d: \(y=kx+b\)
\(\Rightarrow\left\{{}\begin{matrix}0.k+b=1\\k.\left(-\sqrt{3}\right)+b=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=1\\k=\frac{1}{\sqrt{3}}\end{matrix}\right.\)
\(\Rightarrow tan\alpha=k=\frac{1}{\sqrt{3}}\Rightarrow\alpha=30^0\)

bạn dùng công thức này
- gọi góc tạo bởi đường thẳng và trục Ox là ABC thì \(\tan ABC=a\)khi \(a\ge0\)
Thì số đo góc cần tìm là \(\tan ABC=0,5\Rightarrow ABC=26'33\)
áp dụng công thức
gọi ABC là góc tao bởi đường thẳng d với trục Ox thì ta có \(\tan ABC=a\)khi \(a\ge0\)
thì số đo góc cần tìm là tanABC = 0,5\(\Rightarrow\)ABC= 26'33'
-

ĐKXĐ: m<>1, m<>0
a: Để hai đường song song thì \(-\dfrac{2m}{m-1}=\sqrt{3}\)
=>\(-2m=\sqrt{3}m-\sqrt{3}\)
\(\Leftrightarrow m\left(-2-\sqrt{3}\right)=-\sqrt{3}\)
hay \(m=-3+2\sqrt{3}\)
tana=căn 3
nên a=60 độ
b:
\(y=-\dfrac{2m}{m-1}x+\dfrac{2}{m-1}\)
=>\(\dfrac{2m}{m-1}x+y-\dfrac{2}{m-1}=0\)
\(h=d\left(O;d\right)=\dfrac{\left|-\dfrac{2m}{m-1}\cdot0+y\cdot0-\dfrac{2}{m-1}\right|}{\sqrt{\left(\dfrac{2m}{m-1}\right)^2+1^2}}\)
\(=\dfrac{2}{\left|m-1\right|}:\sqrt{\dfrac{4m^2+m^2-2m+1}{\left(m-1\right)^2}}\)
\(=\dfrac{2}{\sqrt{5m^2-2m+1}}\)
Để h lớn nhất thì \(\sqrt{5m^2-2m+1}\) nhỏ nhất
\(5m^2-2m+1=5\left(m^2-\dfrac{2}{5}m+\dfrac{1}{5}\right)\)
\(=5\left(m^2-2\cdot m\cdot\dfrac{1}{5}+\dfrac{1}{25}+\dfrac{4}{25}\right)\)
\(=5\left(m-\dfrac{1}{5}\right)^2+\dfrac{4}{5}>=\dfrac{4}{5}\)
=>\(\sqrt{5\left(m-\dfrac{1}{5}\right)^2+\dfrac{4}{5}}>=\dfrac{2}{\sqrt{5}}\)
Dấu = xảy ra khi m=1/5

ĐKXĐ: m<>1, m<>0
a: Để hai đường song song thì \(-\dfrac{2m}{m-1}=\sqrt{3}\)
=>\(-2m=\sqrt{3}m-\sqrt{3}\)
\(\Leftrightarrow m\left(-2-\sqrt{3}\right)=-\sqrt{3}\)
hay \(m=-3+2\sqrt{3}\)
tana=căn 3
nên a=60 độ
b:
\(y=-\dfrac{2m}{m-1}x+\dfrac{2}{m-1}\)
=>\(\dfrac{2m}{m-1}x+y-\dfrac{2}{m-1}=0\)
\(h=d\left(O;d\right)=\dfrac{\left|-\dfrac{2m}{m-1}\cdot0+y\cdot0-\dfrac{2}{m-1}\right|}{\sqrt{\left(\dfrac{2m}{m-1}\right)^2+1^2}}\)
\(=\dfrac{2}{\left|m-1\right|}:\sqrt{\dfrac{4m^2+m^2-2m+1}{\left(m-1\right)^2}}\)
\(=\dfrac{2}{\sqrt{5m^2-2m+1}}\)
Để h lớn nhất thì \(\sqrt{5m^2-2m+1}\) nhỏ nhất
\(5m^2-2m+1=5\left(m^2-\dfrac{2}{5}m+\dfrac{1}{5}\right)\)
\(=5\left(m^2-2\cdot m\cdot\dfrac{1}{5}+\dfrac{1}{25}+\dfrac{4}{25}\right)\)
\(=5\left(m-\dfrac{1}{5}\right)^2+\dfrac{4}{5}>=\dfrac{4}{5}\)
=>\(\sqrt{5\left(m-\dfrac{1}{5}\right)^2+\dfrac{4}{5}}>=\dfrac{2}{\sqrt{5}}\)
Dấu = xảy ra khi m=1/5

ĐKXĐ: m<>1, m<>0
a: Để hai đường song song thì \(-\dfrac{2m}{m-1}=\sqrt{3}\)
=>\(-2m=\sqrt{3}m-\sqrt{3}\)
\(\Leftrightarrow m\left(-2-\sqrt{3}\right)=-\sqrt{3}\)
hay \(m=-3+2\sqrt{3}\)
tana=căn 3
nên a=60 độ
b:
\(y=-\dfrac{2m}{m-1}x+\dfrac{2}{m-1}\)
=>\(\dfrac{2m}{m-1}x+y-\dfrac{2}{m-1}=0\)
\(h=d\left(O;d\right)=\dfrac{\left|-\dfrac{2m}{m-1}\cdot0+y\cdot0-\dfrac{2}{m-1}\right|}{\sqrt{\left(\dfrac{2m}{m-1}\right)^2+1^2}}\)
\(=\dfrac{2}{\left|m-1\right|}:\sqrt{\dfrac{4m^2+m^2-2m+1}{\left(m-1\right)^2}}\)
\(=\dfrac{2}{\sqrt{5m^2-2m+1}}\)
Để h lớn nhất thì \(\sqrt{5m^2-2m+1}\) nhỏ nhất
\(5m^2-2m+1=5\left(m^2-\dfrac{2}{5}m+\dfrac{1}{5}\right)\)
\(=5\left(m^2-2\cdot m\cdot\dfrac{1}{5}+\dfrac{1}{25}+\dfrac{4}{25}\right)\)
\(=5\left(m-\dfrac{1}{5}\right)^2+\dfrac{4}{5}>=\dfrac{4}{5}\)
=>\(\sqrt{5\left(m-\dfrac{1}{5}\right)^2+\dfrac{4}{5}}>=\dfrac{2}{\sqrt{5}}\)
Dấu = xảy ra khi m=1/5

ĐKXĐ: m<>1, m<>0
a: Để hai đường song song thì \(-\dfrac{2m}{m-1}=\sqrt{3}\)
=>\(-2m=\sqrt{3}m-\sqrt{3}\)
\(\Leftrightarrow m\left(-2-\sqrt{3}\right)=-\sqrt{3}\)
hay \(m=-3+2\sqrt{3}\)
tana=căn 3
nên a=60 độ
b:
\(y=-\dfrac{2m}{m-1}x+\dfrac{2}{m-1}\)
=>\(\dfrac{2m}{m-1}x+y-\dfrac{2}{m-1}=0\)
\(h=d\left(O;d\right)=\dfrac{\left|-\dfrac{2m}{m-1}\cdot0+y\cdot0-\dfrac{2}{m-1}\right|}{\sqrt{\left(\dfrac{2m}{m-1}\right)^2+1^2}}\)
\(=\dfrac{2}{\left|m-1\right|}:\sqrt{\dfrac{4m^2+m^2-2m+1}{\left(m-1\right)^2}}\)
\(=\dfrac{2}{\sqrt{5m^2-2m+1}}\)
Để h lớn nhất thì \(\sqrt{5m^2-2m+1}\) nhỏ nhất
\(5m^2-2m+1=5\left(m^2-\dfrac{2}{5}m+\dfrac{1}{5}\right)\)
\(=5\left(m^2-2\cdot m\cdot\dfrac{1}{5}+\dfrac{1}{25}+\dfrac{4}{25}\right)\)
\(=5\left(m-\dfrac{1}{5}\right)^2+\dfrac{4}{5}>=\dfrac{4}{5}\)
=>\(\sqrt{5\left(m-\dfrac{1}{5}\right)^2+\dfrac{4}{5}}>=\dfrac{2}{\sqrt{5}}\)
Dấu = xảy ra khi m=1/5

ĐKXĐ: m<>1, m<>0
a: Để hai đường song song thì \(-\dfrac{2m}{m-1}=\sqrt{3}\)
=>\(-2m=\sqrt{3}m-\sqrt{3}\)
\(\Leftrightarrow m\left(-2-\sqrt{3}\right)=-\sqrt{3}\)
hay \(m=-3+2\sqrt{3}\)
tana=căn 3
nên a=60 độ
b:
\(y=-\dfrac{2m}{m-1}x+\dfrac{2}{m-1}\)
=>\(\dfrac{2m}{m-1}x+y-\dfrac{2}{m-1}=0\)
\(h=d\left(O;d\right)=\dfrac{\left|-\dfrac{2m}{m-1}\cdot0+y\cdot0-\dfrac{2}{m-1}\right|}{\sqrt{\left(\dfrac{2m}{m-1}\right)^2+1^2}}\)
\(=\dfrac{2}{\left|m-1\right|}:\sqrt{\dfrac{4m^2+m^2-2m+1}{\left(m-1\right)^2}}\)
\(=\dfrac{2}{\sqrt{5m^2-2m+1}}\)
Để h lớn nhất thì \(\sqrt{5m^2-2m+1}\) nhỏ nhất
\(5m^2-2m+1=5\left(m^2-\dfrac{2}{5}m+\dfrac{1}{5}\right)\)
\(=5\left(m^2-2\cdot m\cdot\dfrac{1}{5}+\dfrac{1}{25}+\dfrac{4}{25}\right)\)
\(=5\left(m-\dfrac{1}{5}\right)^2+\dfrac{4}{5}>=\dfrac{4}{5}\)
=>\(\sqrt{5\left(m-\dfrac{1}{5}\right)^2+\dfrac{4}{5}}>=\dfrac{2}{\sqrt{5}}\)
Dấu = xảy ra khi m=1/5
O A B x y 1 d
Đường thẳng d cắt trục Ox tại A(1;0) và cắt trục Oy tại \(B\left(0;\sqrt{3}\right)\)
Ta có: \(tan\widehat{BAO}=\dfrac{OB}{OA}=\dfrac{\sqrt{3}}{1}=\sqrt{3}\Rightarrow\widehat{BAO}=30^0\)
Góc tạo bởi đường thẳng d và trục Ox là góc \(\widehat{BAx}\)
Suy ra \(\widehat{BAx}=180^0-\widehat{BAO}=180^0-30^0=150^0\)
Đs....