Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trả lời: Gọi giá một quyển sách, một quyển vở, một chiếc bút thứ tự là S, V, B đồng. Ta có:
\(S+6V+3B=7700\) (1)
\(8S+6V+6B=16000\) (2)
Nhân (1) với 2 rồi trừ vào (2) ta được:
\(6S-6V=600=>S-V=100\)
Giá một quyển sách nhiều hơn giá một quyển
bit lm bài này k giup tui
vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b
\(\frac{x-4}{y-3}=\frac{4}{3}\Rightarrow\frac{x-4}{4}=\frac{y-3}{3}\)
Áp dụng TC của DTSBN ta có:
\(\frac{x-4}{4}=\frac{y-3}{3}=\frac{x-4-y+3}{4-3}=\frac{5-1}{1}=4\)
Suy ra: (x-4)/4=4 =>x-4=16=>x=20
(y-3)/3=4=>y-3=12=>x=15
x-4/y-3=4/3
=>3.(x-4)=4.(y-3)
=>3x-12=4y-12
=>3x=4y
Mà x-y=5=>x=y+5
=>3.(y+5)=4y
=>3y+15=4y=>4y-3y=15=>y=15
Khi đó x=15+5=20
Vậy x=20;y=15
hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm
Đáp án C
Phương pháp giải: Sử dụng biến cố đối và các quy tắc đếm cơ bản.
Lời giải:
Chọn 3 quyển sách trong 15 quyển sách có 
cách => n(Ω) = 455
Gọi X là biến cố 3 quyển sách được lấy ra có ít nhất một quyển sách là toán.
Và X là biến cố 3 quyển sách được lấy ra không có quyển sách toán. Khi đó, ta xét các trường hợp sau:
TH1. Lấy được 2 quyển lý, 1 quyển hóa => có 
cách
TH2. Lấy được 1 quyển lý, 2 quyển hóa => có 
cách
TH3. Lấy được 3 quyển lý, 0 quyển hóa => có 
cách
TH4. Lấy được 0 quyển lý, 3 quyển hóa => có 
cách
Suy ra số phần tử của biến cố
X
là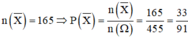 
Vậy xác suất cần tính là 
Đáp án C.
Xếp vị trí từng môn: 3!=6
Xếp vị trí trong tập toán: 5!
Xếp vị trí trong tập lý: 4!
Xếp vị trí trong tập hóa: 3!
=>Có 6.5!.4!.3!