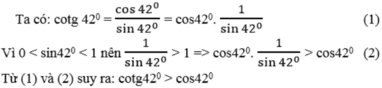KA
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HV
1
TL
1
14 tháng 8 2022
a: \(tan52^0>tan32^0>sin32^0=cos58^0\)
b: \(cot42^0>cos42^0\)
NN
1
15 tháng 9 2015
\(=\sqrt{7^2-2.7.3\sqrt{5}+\left(3\sqrt{5}\right)^2}+\sqrt{7^2+2.7.3\sqrt{5}+\left(3\sqrt{5}\right)^2}\)
\(=\sqrt{\left(7-3\sqrt{5}\right)^2}+\sqrt{\left(7+3\sqrt{5}\right)^2}\)
\(=7-3\sqrt{5}+7+3\sqrt{5}=14\)
AB
0
Y
5 tháng 7 2019
ĐK : \(x\ge-\frac{42}{11}\)
+ Đặt \(t=\sqrt{11x+42}\ge0\) thì pt đã cho trở thành :
\(x^2+t^2=2xt\Leftrightarrow\left(x-t\right)^2=0\)
\(\Leftrightarrow x=t\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt{11x+42}=x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\11x+42=x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x^2-11x-42=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(x-14\right)\left(x+3\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x=14\left(TM\right)\\x=-3\left(KTM\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy x = 4 là nghiệm duy nhất của pt đã cho
2
4 tháng 7 2018
\(\sqrt{94-42\sqrt{5}}-\sqrt{94+42\sqrt{5}}=\sqrt{49-2.7.3\sqrt{5}+45}-\sqrt{49+2.7.3\sqrt{5}+45}=7-3\sqrt{5}-7-3\sqrt{5}=-6\sqrt{5}\)
VI
5
MA
9 tháng 9 2016
Đặt: \(P=\sqrt{94-42\sqrt{5}}-\sqrt{94+42\sqrt{5}}\)
\(P^2=\left(\sqrt{94-42\sqrt{5}}-\sqrt{94+42\sqrt{5}}\right)^2\)
\(P^2=94-42\sqrt{5}-2\sqrt{94-42\sqrt{5}}.\sqrt{94+42\sqrt{5}}+94+42\sqrt{5}\)
\(P^2=188-2\sqrt{\left(94-42\sqrt{5}\right)\left(94+42\sqrt{5}\right)}\)
\(P^2=188-2\sqrt{94^2+3948\sqrt{5}-3948\sqrt{5}-8820}\)
\(P^2=188-2\sqrt{8836-8820}\)
\(P^2=188-2\sqrt{16}\)
\(P^2=188-8\)
\(P^2=180\)
\(P=\orbr{\begin{cases}6\sqrt{5}\\-6\sqrt{5}\end{cases}}\) .
Mà theo bài ra: \(\sqrt{94-42\sqrt{5}}< \sqrt{94+42\sqrt{5}}\)
\(\Rightarrow\sqrt{94-42\sqrt{5}}-\sqrt{94+42\sqrt{5}}< 0\)
\(\Rightarrow P=-6\sqrt{5}\)
9 tháng 9 2016
Làm gì phức tạp thế
94 - 42\(\sqrt{5}\)= 49 - 2×7×3×\(\sqrt{5}\)+ 45 = (7 - \(3\sqrt{5}\))2
Tương tự 94 + 42\(\sqrt{5}\) = (7 + \(3\sqrt{5}\))2
Từ đó suy ra đáp số là 6\(\sqrt{5}\)