Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1: a) Ta có : \(\dfrac{-3}{x}=\dfrac{x}{-27}\Leftrightarrow\left(-3\right).\left(-27\right)=x.x\Leftrightarrow81=x^2\Leftrightarrow9^2=x^2\Leftrightarrow x=9\)
b) Do \(\dfrac{2}{3}\) của x là -150 nên x là: (-150) : \(\dfrac{2}{3}\) = -225
c) \(\dfrac{2}{2.4}+\dfrac{2}{4.6}+...+\dfrac{2}{x\left(x+2\right)}=\dfrac{4}{9}\)
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{x}-\dfrac{1}{x+2}=\dfrac{4}{9}\)
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{x+2}=\dfrac{4}{9}\)
\(\Leftrightarrow\dfrac{1}{x+2}=\dfrac{1}{2}-\dfrac{4}{9}\)
\(\Leftrightarrow\dfrac{1}{x+2}=\dfrac{1}{18}\)
\(\Leftrightarrow x+2=18\)
\(\Leftrightarrow x=16\)
Bài 2:
\(A=\left(\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{999}\right)\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\)
\(A=\left(\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{999}\right)\left(\dfrac{1}{6}-\dfrac{1}{6}\right)\)
\(A=\left(\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{999}\right).0\)
\(A=0\)

\(M=\dfrac{8}{3}\cdot\dfrac{2}{5}\cdot\dfrac{3}{8}\cdot10\cdot\dfrac{19}{92}\\ =\dfrac{8\cdot2\cdot3\cdot10\cdot19}{3\cdot5\cdot8\cdot92}\\ =\dfrac{8\cdot2\cdot3\cdot2\cdot5\cdot19}{3\cdot5\cdot8\cdot2\cdot2\cdot23}\\ =\dfrac{19}{23}\)
\(N=\dfrac{5}{7}\cdot\dfrac{5}{11}+\dfrac{5}{7}\cdot\dfrac{2}{11}-\dfrac{5}{7}\cdot\dfrac{14}{11}\\ =\dfrac{5}{7}\cdot\left(\dfrac{5}{11}+\dfrac{2}{11}-\dfrac{14}{11}\right)\\ =\dfrac{5}{7}\cdot\left(-\dfrac{7}{11}\right)\\ =-\dfrac{5}{11}\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\\ =\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot\left(\dfrac{3}{6}-\dfrac{2}{6}-\dfrac{1}{6}\right)\\ =\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot\left(\dfrac{1}{6}-\dfrac{1}{6}\right)\\ =\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot0\\ =0\)

1. \(A=\dfrac{2\left(\dfrac{1}{5}+\dfrac{1}{7}-\dfrac{1}{9}-\dfrac{1}{11}\right)}{4\left(\dfrac{1}{5}+\dfrac{1}{7}-\dfrac{1}{9}-\dfrac{1}{11}\right)}=\dfrac{2}{4}=\dfrac{1}{2}\)
2. \(B=\dfrac{1^2.2^2.3^2.4^2}{1.2^2.3^2.4^2.5}=\dfrac{1}{5}\)
3.\(C=\dfrac{2^2.3^2.\text{4^2.5^2}.5^2}{1.2^2.3^2.4^2.5.6^2}=\dfrac{125}{36}\)
4.D=\(D=\left(\dfrac{4}{5}-\dfrac{1}{6}\right).\dfrac{4}{9}.\dfrac{1}{16}=\dfrac{19}{30}.\dfrac{1}{36}=\dfrac{19}{1080}\)

1/3+1/6+1/10+...+2/x(x+1)=998/1000
2/6+2/12+2/20+...+2/x(x+1)=998/1000
2[1/2.3+1/3.4+1/4.5+...+1/x(x+1)]=998/1000
2[1/2-1/3+1/3-1/4+1/4-1/5+...+1/x+1/(x+1)]=998/1000
2.[1/2-1/(x+1)]=998/1000
1/2-1/(x+1)=499/1000
1/(x+1)=1/2-499/1000
1/(x+1)=1/1000
=> x=999

a) \(1-\dfrac{1}{2}=\dfrac{1}{2}\)
\(\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{3-2}{6}=\dfrac{1}{6}\)
\(\dfrac{1}{3}-\dfrac{1}{4}=\dfrac{4-3}{12}=\dfrac{1}{12}\)
\(\dfrac{1}{4}-\dfrac{1}{5}=\dfrac{5-4}{20}=\dfrac{1}{20}\)
\(\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{6-5}{30}=\dfrac{1}{30}\)
b) \(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}\)
\(=\left(1-\dfrac{1}{2}\right)+\left(\dfrac{1}{2}-\dfrac{1}{3}\right)+\left(\dfrac{1}{3}-\dfrac{1}{4}\right)+\left(\dfrac{1}{4}-\dfrac{1}{5}\right)+\left(\dfrac{1}{5}+\dfrac{1}{6}\right)\)
\(=1+\left(-\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(-\dfrac{1}{3}+\dfrac{1}{3}\right)+\left(-\dfrac{1}{4}+\dfrac{1}{4}\right)+\left(-\dfrac{1}{5}+\dfrac{1}{5}\right)+-\dfrac{1}{6}\)\(=1+-\dfrac{1}{6}\)
\(=\dfrac{5}{6}\)
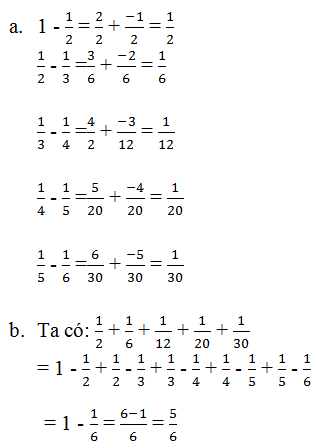
\(\dfrac{1}{1}.\dfrac{1}{2}+\dfrac{1}{2}.\dfrac{1}{3}+\dfrac{1}{3}.\dfrac{1}{4}+...+\dfrac{1}{999}.\dfrac{1}{1000}\\ =\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{999.1000}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{999}-\dfrac{1}{1000}\\ =1-\dfrac{1}{1000}=\dfrac{999}{1000}\)
ta có
1/1.1/2=1-1/2
1/2.1/3=1/2-1/3
1/3.1/4=1/3-1/4
............
1/999.1/1000=1/999-1/1000
Từ đó suy ra
1/1.1/2+1/2-1/3+1/3+.......+1/998.1/999+1/999.1/1000
=1/1-1/2+1/2-1/3+1/3-.....+1/998-1/999+1/999-1/1000
=1-1/1000
=1000/1000-1/1000
=999/1000
nhớ like bạn nhé