Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)
\(A=cos^230^o-sin^230^o=\left(\dfrac{\sqrt{3}}{2}\right)^2-\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2}\);
\(B=cos60^o+sin45^o=\dfrac{1}{2}+\dfrac{\sqrt{2}}{2}\).
Vì vậy \(A< B\).
b)
\(C=\dfrac{2tan30^o}{1-tan^230^o}=\dfrac{2\dfrac{\sqrt{3}}{2}}{1-\left(\dfrac{\sqrt{3}}{2}\right)^2}=\sqrt{3}\).
\(D=\left(-tan135^o\right)tan60^o=-\left(-1\right).\sqrt{3}=\sqrt{3}\).
Vậy \(C=D\).
a)\(\sin^2\alpha+\cos^2\alpha=1\Rightarrow\sin^2\alpha=1-\cos^2\alpha\)
\(\Rightarrow1-2^2=-3\) \(\Rightarrow\cos=-\sqrt{3}\left(0< \alpha< \dfrac{\pi}{2}\right)\)
b) \(\tan\alpha\times\cot\alpha=1\Rightarrow\tan\alpha=\dfrac{1}{\cot\alpha}\Rightarrow\tan=\dfrac{1}{4}\)
a)Do \(0< \alpha< \dfrac{\pi}{2}\) nên các giá trị lượng giác của \(\alpha\) đều dương.
\(cos\alpha=2sin\alpha\)(1)
Nếu \(sin\alpha=0\Rightarrow cos\alpha\) (vô lý).
Vì vậy \(sin\alpha\ne0\) . Từ (1) \(\Rightarrow\dfrac{cos\alpha}{sin\alpha}=2\)\(\Leftrightarrow cot\alpha=2\).
Suy ra: \(tan\alpha=\dfrac{1}{2}\).
\(sin\alpha=\sqrt{\dfrac{1}{1+cot^2\alpha}}=\dfrac{1}{\sqrt{3}}\).
\(cos\alpha=\sqrt{1-sin^2\alpha}=\sqrt{\dfrac{2}{3}}\).
a) Trên hình bên. Cung có số đo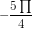 
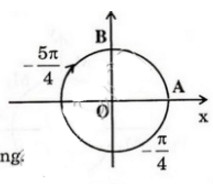
b) Nhận xét rằng 1350 – ( -2250 ) = 3600 . Như vậy cung 1350 và cung -2250 có chung điểm ngọn. Mà cung 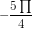cũng là cung -2250 . Vậy cung 1350 cũng chính là cung theo chiều dương
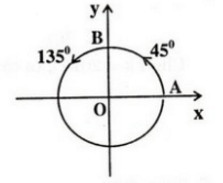
c)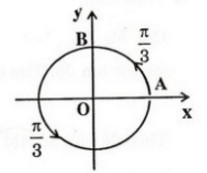 
d)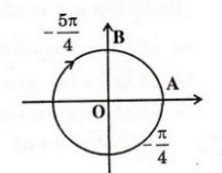 
tam giác mà tới 4 cạnh là không tốt đâu nha bạn
30 A B C 30 120 véc tơ AB véc tơ BC đoạn này được kéo dài từ hướng của véc tơ AB ; để dể sát nhận góc tạo bởi 2 véc tơ AB và BC ? => góc đó là góc cần tìm
từ \(\overrightarrow{AB}\) ta kéo dài ra tạo thành 1 góc ứng với cạnh của \(\overrightarrow{BC}\) và cạnh đó là cạnh cần tìm
ta có cạnh cần tìm \(=180-30=150^o\)
vậy góc tạo bởi 2 véc tơ \(\overrightarrow{AB};\overrightarrow{BC}\) là \(150^o\) \(\Rightarrow\) chọn đáp án \(C\)
a) Do \(90^o< \alpha< 180^o\) nên \(sin\alpha>0;cos\alpha< 0\).
b) Do \(180^o< \alpha< 270^o\) nên \(sin\alpha< 0;cos\alpha< 0\).
c) Do \(270^o< \alpha< 360^o\) nên \(sin\alpha< 0;cos\alpha>0\).
d) \(\alpha=1280^o=3.360^o+200^o\)
\(sin1280^o=sin\left(3.360^o+200^o\right)=sin200^o< 0\).
e)
\(sin\left(-235^o\right)=sin\left(-235^o+360^o\right)=sin125^o>0\).
\(cos\left(-235^o\right)=cos\left(-235^o+360^o\right)=cos125^o< 0\).
d) \(sin\left(-1876\right)=sin\left(-1876^o+1800^o\right)=sin\left(-76^o\right)\)\(=-sin76^o< 0\).
\(cos\left(-1876^o\right)=cos\left(-76^o\right)=cos76^o>0\).
a) Theo giả thiết \(\overrightarrow{a}=\overrightarrow{b}\ne\overrightarrow{0}\) nên giả sử \(\overrightarrow{a}=m\overrightarrow{b}\) suy ra:
\(\overrightarrow{a}=m\overrightarrow{a}\Leftrightarrow\left(1-m\right)\overrightarrow{a}=\overrightarrow{0}\).
\(\Leftrightarrow1-m=0\) (vì \(\overrightarrow{a}\ne\overrightarrow{0}\) ).
\(\Leftrightarrow m=1\).
b) Nếu \(\overrightarrow{a}=-\overrightarrow{b};\overrightarrow{a}\ne\overrightarrow{0}\).
Giả sử \(\overrightarrow{a}=m\overrightarrow{b}\Leftrightarrow\overrightarrow{a}=-m\overrightarrow{a}\)\(\Leftrightarrow\overrightarrow{a}\left(1+m\right)=\overrightarrow{0}\)
\(\Leftrightarrow1+m=0\)\(\Leftrightarrow m=-1\).
c) Do \(\overrightarrow{a}\) , \(\overrightarrow{b}\) cùng hướng nên: \(m>0\).
Mặt khác: \(\overrightarrow{a}=m\overrightarrow{b}\Leftrightarrow\left|\overrightarrow{a}\right|=\left|m\right|.\left|\overrightarrow{b}\right|\)
\(\Leftrightarrow20=5.\left|m\right|\)\(\Leftrightarrow\left|m\right|=4\)
\(\Leftrightarrow m=\pm4\).
Do m > 0 nên m = 4.
d) Do \(\overrightarrow{a},\overrightarrow{b}\) ngược hướng nên m < 0.
\(\left|\overrightarrow{a}\right|=\left|m\right|.\left|\overrightarrow{b}\right|\)\(\Leftrightarrow15=\left|m\right|.3\)\(\Leftrightarrow\left|m\right|=5\)\(\Leftrightarrow m=\pm5\).
Do m < 0 nên m = -5.
e) \(\overrightarrow{a}=\overrightarrow{0};\overrightarrow{b}\ne\overrightarrow{0}\) nên\(\overrightarrow{0}=m.\overrightarrow{b}\). Suy ra m = 0.
g) \(\overrightarrow{a}\ne\overrightarrow{0};\overrightarrow{b}=\overrightarrow{0}\) nên \(\overrightarrow{a}=m.\overrightarrow{0}=\overrightarrow{0}\). Suy ra không tồn tại giá trị m thỏa mãn.
h) \(\overrightarrow{a}=\overrightarrow{0};\overrightarrow{b}=\overrightarrow{0}\) nên \(\overrightarrow{0}=m.\overrightarrow{0}\). Suy ra mọi \(m\in R\) đều thỏa mãn.
gọi vtpt \(\Delta_1\)là \(\overrightarrow{n_1}\)=(m;1)
vtpt\(\Delta_2\) là \(\overrightarrow{n_2}\)=(1;-1)
để hai đường thẳng vuông góc thì \(\overrightarrow{n_1}\)\(\times\)\(\overrightarrow{n_2}\)=\(\overrightarrow{0}\)<=>m\(\times\)1-1=0<=> m=1
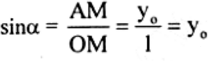
a) \(sin120^o=sin60^o=\dfrac{\sqrt{3}}{2};cos120^o=-cos60^o=-\dfrac{1}{2}\);
\(tan120^o=-\sqrt{3};cot120^o=\dfrac{-1}{\sqrt{3}}\).
b) \(sin150^o=sin30^o=\dfrac{1}{2};cos150^o=-cos30^o=-\dfrac{\sqrt{3}}{2}\).
\(tan150^o=-tan30^o=-\dfrac{\sqrt{3}}{3}\); \(cot150^o=-cot30^o=-\sqrt{3}\).
c)\(sin135^o=sin45^o=\dfrac{\sqrt{2}}{2};cos135^o=-cos45^o=-\dfrac{\sqrt{2}}{2}\).
\(tan135^o=-tan45^o=-1\); \(cot135^o=-1\).
Làm sao bạn tính ra vậy