PA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
1
14 tháng 4 2020
gợi ý nhé:
[-(x-y)2-10(x-y)-25] - 2(y-1)2 + 2010
= -[(x-y)+5]2 - 2(y-1)2 + 2010
tự cậu suy ra MAX nhé
chưa hiểu thì hỏi nhé
T
28 tháng 4 2019
\(A=\left(-x^2-2xy-y^2\right)-2y^2+\left(10x+10y\right)+4y-18\)
\(=-\left(x+y\right)^2+2\left(x+y\right).5-\left(2y^2-4y+2\right)-16\)
\(=-\left[\left(x+y\right)^2-2\left(x+y\right).5+5^2\right]-2\left(y-1\right)^2+9\)
\(=-\left(x+y-5\right)^2-2\left(y-1\right)^2+9\le9\forall x;y\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}x+y-5=0\\y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=5-y\\y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=4\\y=1\end{cases}}\)
Vậy \(A_{max}=9\Leftrightarrow\hept{\begin{cases}x=4\\y=1\end{cases}}\)
LN
2 tháng 12 2015
B=\(x^2+3x+7\)
=>B= \(x^2+2\times\frac{3}{2}x+\frac{9}{4}+\frac{19}{4}\)
=>B=\(\left(x+\frac{3}{2}\right)^2+\frac{19}{4}\)
Vì \(\left(x+\frac{3}{2}\right)^2\ge0\) (Với mọi x)
=>\(\left(x+\frac{3}{2}\right)^2+\frac{19}{4}\ge\frac{19}{4}\) (Với mọi x )
Dấu "='' xảy ra <=> \(x+\frac{3}{2}=0=>x=-\frac{3}{2}\)
Vậy min B bằng 19/4 <=>x=-3/2
Phần b thì mk làm đc n phần a hình như sai đề pn ạ !!!
NT
0
5 tháng 7 2022
a: \(A=-4x^2+10x-23\)
\(=-4\left(x^2-\dfrac{5}{2}x+\dfrac{23}{4}\right)\)
\(=-4\left(x^2-2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}+\dfrac{67}{16}\right)\)
\(=-4\left(x-\dfrac{5}{4}\right)^2-\dfrac{67}{4}< =-\dfrac{67}{4}\)
Dấu '=' xảy ra khi x=5/4
b: \(x^2-2x+3=\left(x-1\right)^2+2>=2\)
=>B<=1/2
Dấu '=' xảy ra khi x=1
MH
1
MH
1
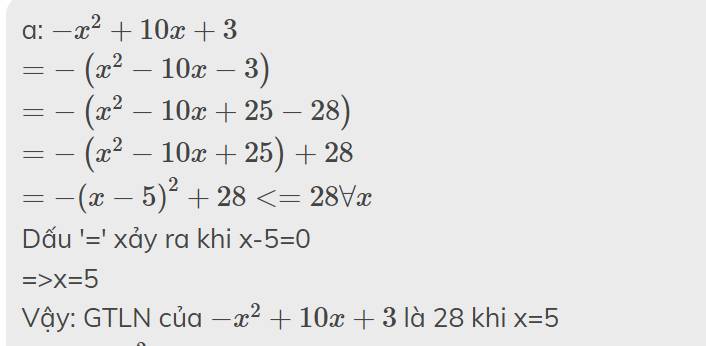
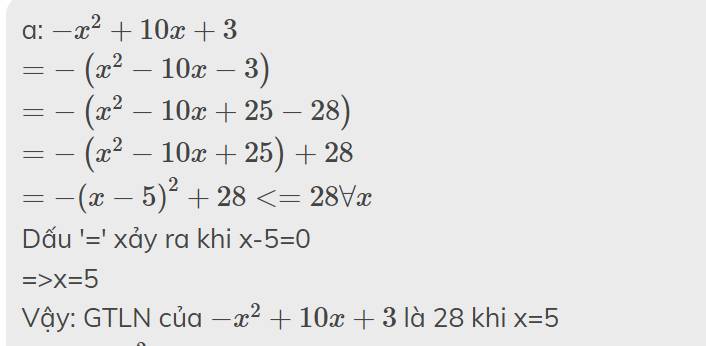
\(Q=\dfrac{23-10x}{x^2+2}=\dfrac{46-20x}{2\left(x^2+2\right)}=\dfrac{25\left(x^2+2\right)-25x^2-20x-4}{2\left(x^2+2\right)}\)
\(=\dfrac{25}{2}-\dfrac{\left(5x+2\right)^2}{2\left(x^2+2\right)}\le\dfrac{25}{2}\)
\(Q_{max}=\dfrac{25}{2}\) khi \(5x+2=0\Rightarrow x=-\dfrac{2}{5}\)