Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(C_n^2-C_n^1=44\Leftrightarrow\frac{n!}{\left(n-2\right)!.2}-\frac{n!}{\left(n-1\right)!}=44\)
\(\Leftrightarrow\frac{n\left(n-1\right)}{2}-n-44=0\Leftrightarrow n^2-3n-88=0\Rightarrow n=11\)
\(\left(x^{\frac{3}{2}}+x^{-4}\right)^{11}=\sum\limits^{11}_{k=0}C_{11}^k\left(x^{\frac{3}{2}}\right)^k.\left(x^{-4}\right)^{11-k}\)
Số hạng tổng quát:
\(C_{11}^k\left(x^{\frac{3}{2}}\right)^k.\left(x^{-4}\right)^{11-k}=C_{11}^kx^{\frac{3k}{2}-44+4k}=C_{11}^kx^{\frac{11k}{2}-44}\)
Số hạng ko chứa \(x\Rightarrow\frac{11k}{2}-44=0\Rightarrow11k=88\Rightarrow k=8\)
Vậy số hạng ko chứa x là \(C_{11}^8=165\)

Theo giả thiết ta có :
\(u_1+u_2=u_1+\frac{1}{4}\left(u_1\right)=24\)
\(\Rightarrow u_1+\frac{1}{4}u_1^2-24=0\)
\(\Leftrightarrow u_1=-12\) V \(u_1=8\)
Vậy có 2 cấp số nhân tương ứng là : 8,16,32,128 hoặc -12,36,-108,-972

De co cho thieu du kien la co bao nhieu so hang ko nhi ?Hay no la 1 csn lui vo han? Neu lui vo han thi lam duoc
\(\left\{{}\begin{matrix}q=4\\\dfrac{1}{u_1}+\dfrac{1}{u_2}+\dfrac{1}{u_3}+...+\dfrac{1}{u_n}+....=2\end{matrix}\right.\)
\(u_2=u_1.q;u_3=u_1.q^2;....;u_n=u_1.q^{n-1}\)
\(\Rightarrow\dfrac{1}{u_1}+\dfrac{1}{u_1.q}+\dfrac{1}{u_1.q^2}+...+\dfrac{1}{u_1.q^{n-1}}+....=2\)
\(\Leftrightarrow\dfrac{1}{u_1}\left(1+\dfrac{1}{q}+\dfrac{1}{q^2}+...+\dfrac{1}{q^{n-1}}+...\right)=2\)
Cần tính tổng trong ngoặc
\(\left\{{}\begin{matrix}u_1'=1\\q'=\dfrac{1}{q}\end{matrix}\right.\)
\(\Rightarrow S'_n=\dfrac{1}{1-q'}=\dfrac{1}{1-\dfrac{1}{4}}=\dfrac{4}{3}\)
\(\Rightarrow u_1=\dfrac{S'_n}{2}=\dfrac{4}{3.2}=\dfrac{2}{3}\)

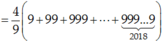
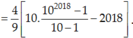
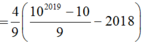


Lời giải:
Đặt \(\underbrace{11...1}_{n}=a\Rightarrow 9a+1=10^n\Rightarrow a=\frac{10^n-1}{9}\Rightarrow \underbrace{44...4}_{n}=4a=\frac{4}{9}(10^n-1)\)
Thay $n=1,2,...,2018$ và đặt tổng cần tính là $T$
Khi đó:
\(T=\frac{4}{9}(10^1-1)+\frac{4}{9}(10^2-1)+\frac{4}{9}(10^3-1)+...+\frac{4}{9}(10^{2018}-1)\)
\(=\frac{4}{9}(10+10^2+10^3+...+10^{2018}-2018)\)
\(10T=\frac{4}{9}(10^2+10^3+...+10^{2019}-20180)\)
Trừ theo vế:
\(9T=10T-T=\frac{4}{9}(10^{2019}-20180-10+2018)=\frac{4}{9}(10^{2019}-18172)\)
\(\Rightarrow T=\frac{4(10^{2019}-18172)}{81}\)