Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Mình sửa lại đề 1 chút: \(x+x^3+x^5+...+x^{101}=P\left(x\right)\)
Số hạng trong dãy là: (101-1):2+1=51
P(-1)=(-1)+(-1)3+(-1)5+...+(-1)101
Vì (-1)2n+1=-1 với n thuộc Z
=> P(-1)=(-1)+(-1)+....+(-1) (có 51 số -1)
=> P(-1)=-51

Bài 1:
a: cho -6x+5=0
⇔ x=\(\dfrac{-5}{-6}\)=\(\dfrac{5}{6}\)
vậy nghiệm của đa thức là:\(\dfrac{5}{6}\)
b: cho x2-2x=0 ⇔ x(x-2)
⇒ x=0 / x-2=0 ⇒ x=0/2
Vậy nghiệm của đa thức là :0 hoặc 2
d : cho x2-4x+3=0 ⇔ x2-x-3x+3=0 ⇔ x(x-1) - 3(x-1)=0 ⇔ (x-3)(x-1)
⇒\(\left[{}\begin{matrix}x-3=0\\x-1=0\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
Vậy nghiệm của đa thức là 1 hoặc 3
f : Cho 3x3+x2=0 ⇔ x2(3x+1)=0
⇒\(\left[{}\begin{matrix}x^2=0\\3x+1=0\end{matrix}\right.\)⇒\(\left[{}\begin{matrix}x=0\\x=\dfrac{-1}{3}\end{matrix}\right.\)
Vậy nghiệm của đa thức là :0 hoặc \(\dfrac{-1}{3}\)
Xin lỗi mình không có thời gian làm hết![]()

A=(3x+7)(2x+3)-(3x-5)(2x+11) =6x2+9x+14x+21-6x2-33x+10x+55 =(6x2-6x2)+(9x+14x-33x+10x)+(21+55) =76
\(A=\left(3x+7\right)\left(2x+3\right)-\left(3x-5\right)\left(2x+11\right)\)
\(\Leftrightarrow A=6x^2+14x+9x+21-\left(6x^2-10x+33x-55\right)\)
\(\Leftrightarrow A=6x^2+23x+21-\left(6x^2+23x-55\right)\)
\(\Leftrightarrow A=6x^2+23x+21-6x^2-23x+55\)
\(\Leftrightarrow A=76\)
\(B=\left(x+1\right)\left(x^2-x-1\right)-\left(x-1\right)\left(x^2+x+1\right)\)
\(\Leftrightarrow B=\left(x+1\right)x^2-x\left(x+1\right)-\left(x+1\right)-\left(x-1\right)x^2-\left(x-1\right)x-\left(x-1\right)\)
\(\Leftrightarrow B=x^3+x^2-x^2-x-x-1-x^3+x^2-x^2+x-x+1\)
\(\Leftrightarrow B=\left(x^3-x^3\right)+\left(x^2-x^2+x^2-x^2\right)+\left(x-x-x-x\right)+\left(1-1\right)\)
\(\Leftrightarrow B=-2x\)

a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3
= x2 - 5 + x4 - 4x3 - x6
Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6
Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1
Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5
b) Ta có:
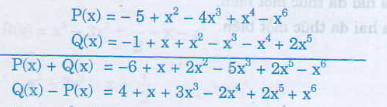 .
.
a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3
= x2 - 5 + x4 - 4x3 - x6
Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6
Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1
Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5
b) Ta có: