Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Thay x = 1 vào biểu thức x2-5x, ta được:
12-5.1 = -4
Vậy -4 là giá trị của thức x2-5x tại x = 1
Thay x = -1 vào biểu thức x2-5x, ta được:
(-1)2-5.(-1) = 6
Vậy 6 là giá trị của biểu thức x2-5x tại x=-1
Thay x = \(\dfrac{1}{2}\) vào biểu thức x2-5x, ta được:
(\(\dfrac{1}{2}\))2-5.\(\dfrac{1}{2}\) = -\(\dfrac{9}{4}\)
Vậy -\(\dfrac{9}{4}\) là giá trị của biểu thức x2-5x tại x =\(\dfrac{1}{2}\)
b) Thay x = -3, y = -5 vào biểu thức 3x2-xy, ta được:
3.(-3)2 - (-3).(-5) = 12
Vậy 12 là giá trị của biểu thức 3x2-xy tại x = -3, y = -5
c) Thay x = 1, y = -3 vào biểu thức 5-xy3, ta được:
5-1.(-3)3 = 32
Vậy 32 là giá trị của biểu thức 5-xy3 tại x = 1, y = -3

a) Thay x = -1 vào biểu thức \(x^2-5\), ta được:
\(\left(-1\right)^2-5=1-5=-4\)
Vậy giá trị biểu thức trên tại x = -1 là -4.
b) Thay x = 1 vào biểu thức \(x^2-3x-5\), ta được:
\(1^2-3.1-5=1-3.1-5=1-3-5=-7\)
Thay x = -1 vào biểu thức \(x^2-3x-5\), ta được:
\(\left(-1\right)^2-3.\left(-1\right)-5=1-3.\left(-1\right)-5=1+3-5=-1\)
Vậy giá trị của biểu thức trên tại x = 1 là -7, tại x = -1 là -1.
a) Thay x = -1 vào biểu thức x2 - 5, ta được:
(-1)2 - 5 = -4
Vậy -4 là giá trị của biểu thức x2-5 tại x = -1
b) Thay x = 1 vào biểu thức x2 - 3x -5, ta được: 12 - 3.1 - 5 = -7
Vậy -7 là giá trị của biểu thức x2-3x-5 tại x = 1
Thay x = -1 vào biểu thức x2 - 3x - 5, ta được: (-1)2 - 3.(-1) - 5 = -1
Vậy -1 là giá trị của biểu thức x2-3x-5 tại x = -1

a) \(5x^2y^2\) tại \(x=-1;y=-\dfrac{1}{2}\)
Tại \(x=-1;y=-\dfrac{1}{2}\) ta có:
\(5.\left(-1\right)^2.\left(-\dfrac{1}{2}\right)^2\) = \(\dfrac{5}{4}\)
b) \(-\dfrac{1}{2}x^2y^3\) tại \(x=1;y=-2\)
Tại \(x=1;y=-2\) ta có:
\(-\dfrac{1}{2}.1^2.\left(-2\right)^3\) = 4
c)\(\dfrac{2}{3}x^2y\) tại x = -3; y = -1
Tại x = -3; y = -1, ta có:
\(\dfrac{2}{3}.\left(-3\right)^2.\left(-1\right)\) = -6

a, Ta có : \(P\left(x\right)=5x^4-3x^2+3x-1-5x^4+4x^2-x-x^2+2\)
\(=2x+1\)
b,* Thay x = 0 vào biểu thức trên ta có : \(2.0+1=1\)
Vậy nếu x = 0 thì biểu thức nhận giá trị 1
* Thay x = -1 vào biểu thức trên ta có : \(2\left(-1\right)+1=-2+1=-1\)
Vậy nếu x = -1 thì biểu thức nhận giá trị là -1
* Thay x = 1/2 vào biểu thức trên ta có : \(2.\frac{1}{2}+1=1+1=2\)
Vậy nếu x = 1/2 thì biểu thức nhận giá trị là 2
c, Ta có \(P\left(x\right)=0\)hay \(2x+1=0\Leftrightarrow x=-\frac{1}{2}\)
Ta có \(P\left(x\right)=1\)hay \(2x+1=1\Leftrightarrow x=0\)

bài 1 :
a) vì x + 1,5 luôn lớn hơn hoặc bằng 0 mà để x+1,5 đạt giá trị nhỏ nhất => x + 1,5 = 0=> x=-1,5
b) vì x- 2 luôn lớn hơn hoặc bằng 0 mà để x-2 - 9,10 đạt gtri nhỏ nhất => x- 2 = 0=> x=2
Câu 1 : Bài giải
a, \(\text{ }\text{Do }\left|x+1,5\right|\ge0\) Dấu " = " xảy ra khi \(x+1,5=0\text{ }\Rightarrow\text{ }x=-1,5\)
\(\Rightarrow\text{ }Min\text{ }\left|x+1,5\right|=0\text{ khi }x=-1,5\)
b, \(\left|x-2\right|-9,10\) đạt GTNNN khi \(\left|x-2\right|\) đạt GTNN
Mà \(\left|x-2\right|\ge0\)Dấu " = " xảy ra khi \(x-2=0\) \(\Rightarrow\text{ }x=2\)
\(\Rightarrow\text{ }\left|x-2\right|-9,10\ge-9,10\)
\(\text{Vậy }Min\text{ }\left|x-2\right|-9,10=-9,10\text{ khi }x=2\)
Câu 2 : Bài giải
a, Do \(-\left|2x-1\right|\le0\) Dấu " = " xảy ra khi \(-\left|2x-1\right|=0\text{ }\Rightarrow\text{ }2x-1=0\text{ }\Rightarrow\text{ }x=\frac{1}{2}\)
Vậy \(Max\text{ }-\left|2x-1\right|=0\text{ khi }x=\frac{1}{2}\)
b, Do \(4-\left|5x+3\right|\le4\text{ }\)
Dấu " = " xảy ra khi \(4-\left|5x+3\right|=4\text{ }\Rightarrow\text{ }\left|5x+3\right|=0\text{ }\Rightarrow\text{ }5x+3=0\text{ }\Rightarrow\text{ }x=-\frac{3}{5}\)
\(\text{Vậy }Max\text{ }4-\left|5x+3\right|=4\text{ khi }x=-\frac{3}{5}\)
c, \(\frac{1}{8}-\left|x+3\right|\le\frac{1}{8}\) Dấu " = " xảy ra khi \(\frac{1}{8}-\left|x+3\right|=\frac{1}{8}\text{ }\Rightarrow\text{ }\left|x+3\right|=0\text{ }\Rightarrow\text{ }x+3=0\text{ }\Rightarrow\text{ }x=-3\)
\(\text{Vậy }Max\text{ }\frac{1}{8}-\left|x+3\right|=\frac{1}{8}\text{ khi }x=-3\)

Bài 1:
|\(x\)| = 1 ⇒ \(x\) \(\in\) {-\(\dfrac{1}{3}\); \(\dfrac{1}{3}\)}
A(-1) = 2(-\(\dfrac{1}{3}\))2 - 3.(-\(\dfrac{1}{3}\)) + 5
A(-1) = \(\dfrac{2}{9}\) + 1 + 5
A (-1) = \(\dfrac{56}{9}\)
A(1) = 2.(\(\dfrac{1}{3}\) )2- \(\dfrac{1}{3}\).3 + 5
A(1) = \(\dfrac{2}{9}\) - 1 + 5
A(1) = \(\dfrac{38}{9}\)
|y| = 1 ⇒ y \(\in\) {-1; 1}
⇒ (\(x;y\)) = (-\(\dfrac{1}{3}\); -1); (-\(\dfrac{1}{3}\); 1); (\(\dfrac{1}{3};-1\)); (\(\dfrac{1}{3};1\))
B(-\(\dfrac{1}{3}\);-1) = 2.(-\(\dfrac{1}{3}\))2 - 3.(-\(\dfrac{1}{3}\)).(-1) + (-1)2
B(-\(\dfrac{1}{3}\); -1) = \(\dfrac{2}{9}\) - 1 + 1
B(-\(\dfrac{1}{3}\); -1) = \(\dfrac{2}{9}\)
B(-\(\dfrac{1}{3}\); 1) = 2.(-\(\dfrac{1}{3}\))2 - 3.(-\(\dfrac{1}{3}\)).1 + 12
B(-\(\dfrac{1}{3};1\)) = \(\dfrac{2}{9}\) + 1 + 1
B(-\(\dfrac{1}{3}\); 1) = \(\dfrac{20}{9}\)
B(\(\dfrac{1}{3};-1\)) = 2.(\(\dfrac{1}{3}\))2 - 3.(\(\dfrac{1}{3}\)).(-1) + (-1)2
B(\(\dfrac{1}{3}\); -1) = \(\dfrac{2}{9}\) + 1 + 1
B(\(\dfrac{1}{3}\); -1) = \(\dfrac{20}{9}\)
B(\(\dfrac{1}{3}\); 1) = 2.(\(\dfrac{1}{3}\))2 - 3.(\(\dfrac{1}{3}\)).1 + (1)2
B(\(\dfrac{1}{3}\); 1) = \(\dfrac{2}{9}\) - 1 + 1
B(\(\dfrac{1}{3}\);1) = \(\dfrac{2}{9}\)

a) Ta có: \(M=\frac{2x+5}{x+1}=\frac{2\left(x+1\right)+3}{x+1}=\frac{2x+2+3}{x+1}\)
Vì \(2x+2⋮\left(x+1\right)\Rightarrow3⋮\left(x+1\right)\)
Nên \(x+1\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
\(\Rightarrow x=\left\{0;-2;2;-4\right\}\)
b) Tương tự
*Thay x = 1 vào biểu thức, ta có: 12 – 5.1 = 1 – 5 = -4
Vậy giá trị của biểu thức x2 – 5x tại x = 1 là -4.
*Thay x = -1 vào biểu thức, ta có: (-1)2 – 5.(-1) = 1 + 5 = 6
Vậy giá trị của biểu thức x2 – 5x tại x = 1 là 6.
*Thay x = 1/2 vào biểu thức, ta có: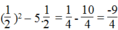
Vậy giá trị của biểu thức x2 – 5x tại x = 1/2 là -9/4 .