OLM ưu đãi đặc biệt gói SVIP 18 THÁNG dành cho nhà trường, đăng kí ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
CC
chỉ có thể là mình
29 tháng 10 2016 - olm

tính gia trị của biếu thức sau

E=\(\frac{\left(13\frac{1}{4}-2\frac{5}{7}-10\frac{5}{6}\right)\times230\frac{1}{25}+46\frac{3}{4}}{\left(1\frac{3}{7}+\frac{10}{3}\right)\div\left(12\frac{1}{3}-14\frac{2}{7}\right)}\)

GIẢI HỘ MILK NHA AI LÀM được MIK TK 3 CAI THANKS
#Hỏi cộng đồng OLM #Toán lớp 7
0
F
Fenny
23 tháng 9 2020 - olm

Tính giá trị các biểu thức sau

d) \(\frac{72^3.54^2}{108^4}\)

e) \(\frac{3^{10}.11+3^{10}.5}{3^9.2^4}\)
#Hỏi cộng đồng OLM #Toán lớp 7
1
AF
All For E
23 tháng 9 2020

                                                            Bài giải

\(d,\text{ }\frac{72^3\cdot54^2}{108^4}=\frac{3^6\cdot2^9\cdot3^6\cdot2^2}{3^{12}\cdot2^8}=2^3=9\)

\(e,\text{ }\frac{3^{10}\cdot11+3^{10}\cdot5}{3^9\cdot2^4}=\frac{3^{10}\left(11+5\right)}{3^9\cdot2^4}=\frac{3\cdot16}{2^4}=\frac{3\cdot2^4}{2^4}=3\)

Đúng(0)
TX
Trang Xù
11 tháng 2 2018 - olm
1. Cho biểu thức:A=2x2−5x−5A=2x2−5x−5Tính giá trị của biểu thức x=−2,x=12x=−2,x=122.Cho biểu thức:D=(x2−1).(x2−2).(x2−3).....(x2−2015)D=(x2−1).(x2−2).(x2−3).....(x2−2015)Tính giá trị biểu thức D tại x=(x2+2010).(x−10)=0x=(x2+2010).(x−10)=03.Tìm giá trị nhỏ nhất của biểu thức:a.A=(x−3)2+9a.A=(x−3)2+9b.(x−1)+(y+2)2+10(x−1)+(y+2)2+10c.|x−1|+(2y−1)4+1|x−1|+(2y−1)4+14.Tính giá trị lớn nhất của...
Đọc tiếp

1. Cho biểu thức:A=2x2−5x−5A=2x2−5x−5

Tính giá trị của biểu thức x=−2,x=12x=−2,x=12

2.Cho biểu thức:D=(x2−1).(x2−2).(x2−3).....(x2−2015)D=(x2−1).(x2−2).(x2−3).....(x2−2015)

Tính giá trị biểu thức D tại x=(x2+2010).(x−10)=0x=(x2+2010).(x−10)=0

3.Tìm giá trị nhỏ nhất của biểu thức:

a.A=(x−3)2+9a.A=(x−3)2+9

b.(x−1)+(y+2)2+10(x−1)+(y+2)2+10

c.|x−1|+(2y−1)4+1|x−1|+(2y−1)4+1

4.Tính giá trị lớn nhất của biểu thức:

a.P=−2.(x−3)2+5P=−2.(x−3)2+5

b.Q=5(x−14)2+21Q=5(x−14)2+21

5.Tìm x thuộc Z để A=x−5x−3A=x−5x−3 thuộc Z
#Hỏi cộng đồng OLM #Toán lớp 7
0
NB
nguyễn ban mai
1 tháng 4 2019 - olm
1. Chứng minh rằng : ba đơn thức -1/2 xy2  ; -3/4 x3y ; 2y không thể cùng có giá trị âm 2. A= 3a - 2b / a- 3b với a/b = 10/3  ( tính giá trị biểu thức đại số)3. a) tìm giá trị nguyên của x để biểu thức sau nhận gái trị nguyên: A= x + 4/ x+2 : B= 2x+ 2 / x+1b) tìm giá trị nhỏ  nhất của biểu thức: A= ( x - 2) 2 + /y - 1/ -4/.../ là dấu giá trị tuyệt đối4.Cho biết M + (2x2 + 2xy + y2 ) = 3x2 + 2xy + y2+...
Đọc tiếp

1. Chứng minh rằng : ba đơn thức -1/2 xy2  ; -3/4 x3y ; 2y không thể cùng có giá trị âm 

2. A= 3a - 2b / a- 3b với a/b = 10/3  ( tính giá trị biểu thức đại số)

3. a) tìm giá trị nguyên của x để biểu thức sau nhận gái trị nguyên: 

A= x + 4/ x+2 : B= 2x+ 2 / x+1

b) tìm giá trị nhỏ  nhất của biểu thức: A= ( x - 2) 2 + /y - 1/ -4

/.../ là dấu giá trị tuyệt đối

4.Cho biết M + (2x2 + 2xy + y2 ) = 3x2 + 2xy + y2+ 1

a) Tìm đa thức M

b) Với giá trị nòa của x ( x > 0) thì M= 17

Mọi người  giúp mình đi...
#Hỏi cộng đồng OLM #Toán lớp 7
0
NN
nguyễn ngọc khánh vân
30 tháng 10 2016 - olm

Giá trị lớn nhất của biếu thức 5/ 4(x - 3)2 + 2
#Hỏi cộng đồng OLM #Toán lớp 7
1
SL
Sát Long Nhân Natsu
30 tháng 10 2016

ko có gt lớn nhất

Đúng(0)
HN
Hoa Ngọc Lan
10 tháng 6 2017 - olm

Tính giá trị của các biểu thức sau:

a,\(\frac{2^{30}.5^7+2^{13}.5^{27}}{2^{27}.5^7+2^{10}.5^{27}}\)

b,\(\frac{81.2^2+3^4+20.9^2}{16.3^2+45+2^2.9}\)
#Hỏi cộng đồng OLM #Toán lớp 7
2
DK
Đỗ Kim Lâm
10 tháng 6 2017

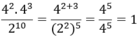
a,        \(\frac{2^{30}.5^7+2^{13}.5^{27}}{2^{27}.5^7+2^{10}.5^{27}}=\frac{2^{13}.\left(2^{17}.5^7+5^{27}\right)}{2^{10}.\left(2^{17}.5^7+5^{27}\right)}=\frac{2^{13}}{2^{10}}=2^3=8\).

b,        \(\frac{81.2^2+3^4+20.9^2}{16.3^2+45+2^2.9}=\frac{3^4.2^2+3^4+20.3^4}{16.3^2+3^2.5+2^2.3^2}=\frac{3^4.\left(2^2+1+20\right)}{3^2.\left(16+5+2^2\right)}=\frac{3^4.25}{3^2.25}=\frac{3^4}{3^2}=3^2=9\)

Đúng(0)
NK
Nguyễn Kiên
10 tháng 6 2017

a : 8

b : 9

Đúng(0)
YD
_ Yuki _ Dễ thương _
1 tháng 3 2017

Giá trị biếu thức \(A=\frac{1+2+3+...+103+104+105}{1-2+3-4+...+103-105+105}\)
#Hỏi cộng đồng OLM #Toán lớp 7
2
KS
Kudo shinichi
2 tháng 3 2017

105 nhe bn!mk giai sau nhe!

Đúng(0)
KS
Kudo shinichi
2 tháng 3 2017

Đặt tử số là B=1+2+3+....+105

Số các số hạng của B là

(105-1):1+1=105(số)

Tổng B là:

(105+1)x105:2=5565

Đặt mẫu số là C =1-2+3-4+...+103-104+105

C=(1-2)+(3-4)+...+(103-104)+105

C=-1+(-1)+...+(-1)(52 số hạng) + 105

C=-52 + 105

C=53

Vậy A=\(\dfrac{B}{C}\)=\(\dfrac{5565}{53}=105\)

Đúng(0)
CC
Cục Chiên Đáng êu
28 tháng 8 2016 - olm

Với giá trị nào của x, biểu thức sau đạt giá trị nhỏ nhất:

a) C= -3 +\(\left|\frac{3}{4}x-\frac{2}{5}\right|\)

b) D= 10 - \(\frac{1}{3+\left|x-2\right|}\)
#Hỏi cộng đồng OLM #Toán lớp 7
1
MA
Minh Anh
28 tháng 8 2016

\(C=-3+\left|\frac{3}{4}x-\frac{2}{5}\right|\Leftrightarrow\left|\frac{3}{4}x-\frac{2}{5}\right|-3\) . Có: \(\left|\frac{3}{4}x-\frac{2}{5}\right|\ge0\)

\(\Rightarrow\left|\frac{3}{4}x-\frac{2}{5}\right|-3\ge-3\) . Dấu = xảy ra khi: \(\left|\frac{3}{4}x-\frac{2}{5}\right|=0\Rightarrow x=\frac{8}{15}\)

Vậy: \(Min_C=-3\) tại \(x=\frac{8}{15}\)

Đúng(0)
HP
Huy Phan
18 tháng 6 2016

Tìm giá trị các biểu thức sau :  \(\frac{4^2.4^3}{2^{10}}\)
#Hỏi cộng đồng OLM #Toán lớp 7
5
NT
Nguyễn Trần An Thanh
18 tháng 6 2016

\(\frac{4^2.4^3}{2^{10}}=\frac{2^4.2^6}{2^{10}}=\frac{2^{10}}{2^{10}}=1\)

Đúng(0)
DM
Đặng Minh Triều
18 tháng 6 2016

\(\frac{4^2.4^3}{2^{10}}=\frac{4^5}{2^{10}}=\frac{\left(2^2\right)^5}{2^{10}}=\frac{2^{10}}{2^{10}}=1\)

Đúng(0)
TC
Tui cuồg Oppa Song Joong Ki đấy
2 tháng 7 2017 - olm

Tính giá trị biểu thức :\(\frac{7}{10}+\frac{7}{10^2}+\frac{7}{10^3}+\frac{7}{10^4}+...\)
#Hỏi cộng đồng OLM #Toán lớp 7
2
TT
Thanh Tùng DZ
2 tháng 7 2017

đặt \(A=\frac{7}{10}+\frac{7}{10^2}+\frac{7}{10^3}+\frac{7}{10^4}\)

\(A=7.\left(\frac{1}{10}+\frac{1}{10^2}+\frac{1}{10^3}+\frac{1}{10^4}\right)\)

Lại đặt \(B=\frac{1}{10}+\frac{1}{10^2}+\frac{1}{10^3}+\frac{1}{10^4}\)

\(10B=1+\frac{1}{10}+\frac{1}{10^2}+\frac{1}{10^3}\)

\(10B-B=\left(1+\frac{1}{10}+\frac{1}{10^2}+\frac{1}{10^3}\right)-\left(\frac{1}{10}+\frac{1}{10^2}+\frac{1}{10^3}+\frac{1}{10^4}\right)\)

\(9B=1-\frac{1}{10^4}\)

\(\Rightarrow B=\frac{1-\frac{1}{10^4}}{9}\)

\(\Rightarrow A=7.\frac{1-\frac{1}{10^4}}{9}=\frac{7.\left(1-\frac{1}{10^4}\right)}{9}\)

Đúng(0)
TC
Tui cuồg Oppa Song Joong Ki đấy
2 tháng 7 2017

Nhưng có vô hạn số hạng thì sao bạn

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP