
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1.\)
\(-17-\left(x-3\right)^2\)
Ta có: \(\left(x-3\right)^2\ge0\)với \(\forall x\)
\(\Leftrightarrow-\left(x-3\right)^2\le0\)với \(\forall x\)
\(\Leftrightarrow17-\left(x-3\right)^2\le17\)với \(\forall x\)
Dấu '' = '' xảy ra khi:
\(\left(x-3\right)^2=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
Vậy \(Max=-17\)khi \(x=3\)
\(2.\)
\(A=x\left(x+1\right)+\frac{3}{2}\)
\(A=x^2+x+\frac{3}{2}\)
\(A=\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\)
\(\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
\(\Leftrightarrow\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
Vậy \(Max=\frac{5}{4}\)khi \(x=\frac{-1}{2}\)

1. ĐKXĐ: \(x\ne\pm1\)
2. \(A=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right)\cdot\dfrac{x+1}{2}\)
\(=\dfrac{\left(x+1\right)^2-\left(x-3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{x^2+2x+1-x^2+4x-3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{6x-2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{2\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x-3}{x-1}\)
3. Tại x = 5, A có giá trị là:
\(\dfrac{5-3}{5-1}=\dfrac{1}{2}\)
4. \(A=\dfrac{x-3}{x-1}\) \(=\dfrac{x-1-3}{x-1}=1-\dfrac{3}{x-1}\)
Để A nguyên => \(3⋮\left(x-1\right)\) hay \(\left(x-1\right)\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\left(tmđk\right)\\x=0\left(tmđk\right)\\x=4\left(tmđk\right)\\x=-2\left(tmđk\right)\end{matrix}\right.\)
Vậy: A nguyên khi \(x=\left\{2;0;4;-2\right\}\)

a:
ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
b: \(A=\left(\dfrac{x-2}{2x-2}+\dfrac{3}{2x-2}-\dfrac{x+3}{2x+2}\right):\left(1-\dfrac{x-3}{x+1}\right)\)
\(=\left(\dfrac{x-2}{2\left(x-1\right)}+\dfrac{3}{2\left(x-1\right)}-\dfrac{x+3}{2\left(x+1\right)}\right):\dfrac{x+1-x+3}{x+1}\)
\(=\dfrac{\left(x-2\right)\left(x+1\right)+3\left(x+1\right)-\left(x+3\right)\left(x-1\right)}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{x^2-x-2+3x+3-x^2-2x+3}{2\left(x-1\right)}\cdot\dfrac{1}{2}\)
\(=\dfrac{-2}{4\left(x-1\right)}=\dfrac{-1}{2\left(x-1\right)}\)
Khi x=2005 thì \(A=\dfrac{-1}{2\cdot\left(2005-1\right)}=-\dfrac{1}{4008}\)
Vì x=1 không thỏa mãn ĐKXĐ
nên khi x=1 thì A không có giá trị
c: Để A=-1002 thì \(\dfrac{-1}{2\left(x-1\right)}=-1002\)
=>\(2\left(x-1\right)=\dfrac{1}{1002}\)
=>\(x-1=\dfrac{1}{2004}\)
=>\(x=\dfrac{1}{2004}+1=\dfrac{2005}{2004}\left(nhận\right)\)

a: Ta có: |x+4|=1
=>x+4=1 hoặc x+4=-1
=>x=-3(loại) hoặc x=-5
Khi x=-5 thì \(A=\dfrac{\left(-5\right)^2-5}{3\left(-5+3\right)}=\dfrac{20}{3\cdot\left(-2\right)}=\dfrac{-10}{3}\)
b: \(B=\dfrac{x-1+x+1-3+x}{\left(x-1\right)\left(x+1\right)}=\dfrac{3x-3}{\left(x-1\right)\left(x+1\right)}=\dfrac{3}{x+1}\)

Điều kiện xác định của phân thức: x ≠ 0
Với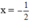 thỏa mãn ĐKXĐ của biến nên thay
thỏa mãn ĐKXĐ của biến nên thay 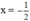 vào phân thức
vào phân thức 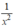 ta được:
ta được: