NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MB
Cho hình thoi ABCD có diện tích bằng 120cm2 , tổng 2 đường chéo bằng 34cm . Tính đường cao hình thoi
0
CM
10 tháng 7 2019
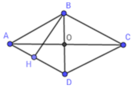
Giả sử hình thoi ABCD, đường chéo AC vuông góc với BD tại O, AC = 20 cm; BD = 15 cm.
Gọi BH là đường cao hình thoi kẻ từ đỉnh B.
Ta có: DO = 1 2 BD = 1 2 .15 = 7,5 (cm);
AO = 1 2 AC = 1 2 .20 = 10 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOD vuông tại O ta có:
AD = A O 2 + O D 2 = 10 2 + 7 , 5 2 = 12,5 (cm)
SABCD = 1 2 BD. AC = 1 2 15.20 = 24 (cm2)
SABCD = BH. AD => BH = S A B C D A D = 150 12 , 5 = 12 (cm)
Đáp án cần chọn là: A
CM
1 tháng 8 2019
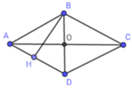
Giả sử hình thoi ABCD, đường chéo AC vuông góc với BD tại O, AC = 8 cm; BD = 6 cm.
Gọi BH là đường cao hình thoi kẻ từ đỉnh B.
Ta có: DO = 1 2 BD = 1 2 .6 = 3 (cm);
AO = 1 2 AC = 1 2 .8 = 4 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOD vuông tại O ta có:
AD = A O 2 + O D 2 = 4 2 + 3 2 = 5 (cm)
SABCD = 1 2 BD. AC = 1 2 6.8 = 24 (cm2)
SABCD = BH. AD => BH = S A B C D A D = 24 5 = 4, 8 (cm)
Đáp án cần chọn là: B
17 tháng 8 2016
Gọi O là giao điểm 2 đường chéo AC và BD.
Vì AC=8 cm, BD=6cm
\(\Rightarrow\)OA=4cm, OB=3cm\(\Rightarrow\)AB=5cm
Chu vi đáy: 2p=5.4=20 (cm)
\(S_{xq}=20\cdot7=170\left(cm^2\right)\)
\(S_{đáy}=\frac{AC\cdot BD}{2}=\frac{8\cdot6}{2}=24\left(cm^2\right)\)
\(\Rightarrow V=S_{đáy}\cdot h=24\cdot7=168\left(cm^3\right)\)
26 tháng 12 2021
a: Độ dài đường chéo là \(5\sqrt{2}\left(cm\right)\)
3 tháng 5 2017
A B O C D H
Gọi hình thoi đó là ABCD
Hai đường chéo BD và AC cắt nhau và vuông góc tại O
Kẻ đường cao AH (H\(\in DC\))
a. SABCD=\(\dfrac{1}{2}.AC.BD=\dfrac{1}{2}.12.16=96\left(cm^2\right)\)
Vậy diện tích hình thoi đó là 96 cm2
b. Ta có: AO=OC=\(\dfrac{AC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
OD=OB=\(\dfrac{BD}{2}=\dfrac{16}{2}=8\left(cm\right)\)
Xét \(\Delta DAO\) có \(\widehat{DOA}=90^o\)
=> OD2+AO2=AD2 (định lý Py-ta-go)
hay: 82+62=AD2
=> AD2=100
=> AD=10 (cm)
Vậy độ dài một cạnh của hình thoi đó là 10 cm
c. Ta có: SABCD=AH.DC
=> AH=\(\dfrac{S_{ABCD}}{DC}=\dfrac{96}{10}=9,6\left(cm\right)\)
Vậy độ dài đường cao của hình thoi đó là 9,6 cm
đụ má đứa tâm vat