Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath

AB-BC<AC<AB+BC và DA-CD<AC<DA+CD
=>2<AC<18 và 16<AC<39
=>AC=17cm
BC-CD<BD<BC+CD và DA-AB<BD<DA+AB
=>3<BD<13 và 11<BD<21
=>BD=12cm

gọi chiều dài là x(m)(x>0)
thì chiều rộng : x-1(m)
vì độ dài mỗi đường chéo Của hình chữ nhật đó là 5m
=>pt: x^2+(x-1)^2=5^2
<=>x^2+x^2-2x+1-25=0
<=>2x^2-2x-24=0=>\(\Delta=\left(-2\right)^2-4\left(-24\right)2=196>0\)
=>\(\left\{{}\begin{matrix}x1=\dfrac{2+\sqrt{196}}{2.2}=4\left(TM\right)\\x2=\dfrac{2-\sqrt{196}}{2.2}=-3\left(loai\right)\end{matrix}\right.\)=> chiều dài là 4m , chiều rộng 3m
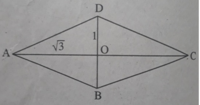
Coi đường chéo AC = 2 3 , đường chéo BD = 2 thì để ý rằng AC và BD vuông góc, ta có
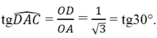
Nên ∠ (DAC) = 30 ° từ đó góc A của hình thoi là 60 ° . Suy ra ∠ C = 60 ° còn ∠ B = ∠ D = 120 °
Diện tích hình thoi là:
\(\frac{18.24}{2}=216cm^2\)
Độ dài các cạnh cơ mà