Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Cho hình thoi ABCD có cạnh AB = 6cm, ∠A = 600

+ ABCD là hình thoi ⇒ ΔBAD cân tại A. Mà ∠A = 600 nên ΔABD là tam giác đều ⇒ BD = AB = 6cm
+ AC ⊥ BD và BI = ID = 3cm
Trong tam giác vuông AIB áp dụng định lý pitago
AI2 = AB2 – IB2 = 36 – 9 = 27 ⇒ AI = √27 (cm)
Suy ra: AC = 2AI = 2√27 (cm)
Vậy SABCD = 1/2AC.BD = 1/2.2√27 .6 = 12√27 (cm2)

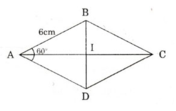
Cho hình thoi ABCD có cạnh AB = 6cm, góc ∠A = 60o.
- Cách 1:
ΔABD là tam giác đều nên BD = AB = 6cm
I là giao điểm của AC và BD => AI ⊥ DB
⇒ AI là đường cao của tam giác đều ABD nên
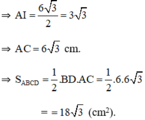
- Cách 2:
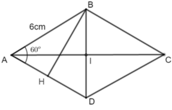
Khi đó ΔABD là tam giác đều. Từ B vẽ BH ⊥ AD thì HA = HD.
Nên tam giác vuông AHB là nửa tam giác đều.
BH là đường cao tam giác đều cạnh 6cm, nên
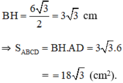

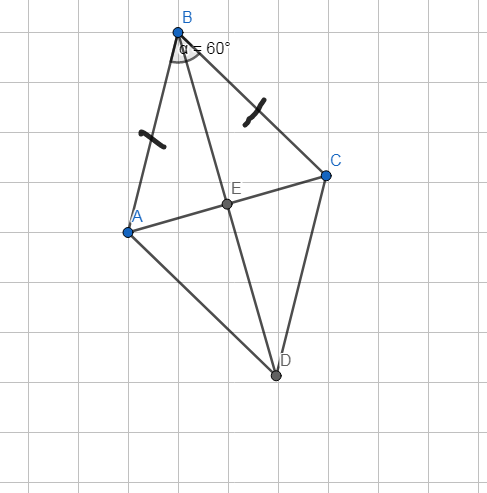
Ta có : AB=BC (ABCD là hình thoi)
=> Tam giác ABC cân tại B
Mà góc B =60o
=> Tam giác ABC đều.
=> AB=BC=CA=6cm
BD=2BE=2.\(\dfrac{\sqrt{3}}{2}\).6=6\(\sqrt{3}\)cm (bạn tự c/m nhé, nó không khó đâu).
SABCD=\(\dfrac{1}{2}\).6.6.\(\sqrt{3}\)=18\(\sqrt{3}\)