Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Từ chu vi tính được cạnh tam giác đều là 30 : 3 = 10 ( cm)
Kẻ đường cao AH xuống BC, H thuộc BC
Dùng Pytago tìm được AH = \(5\sqrt{3}\)
Diện tích tam giác ABC là AH . BC = \(50\sqrt{3}\)
Vậy ...

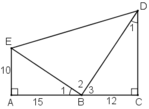
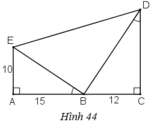
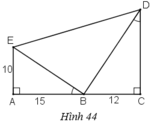
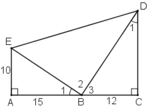
a) + ΔABE vuông tại A.
+ ΔBCD vuông tại C.
+ Ta có:
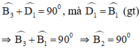
Vậy ΔBED vuông tại B.
b) + Áp dụng định lý Pytago trong ΔABE vuông tại A ta có:
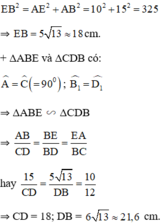
+ Áp dụng định lý Pytago trong ΔEBD vuông tại B ta có:
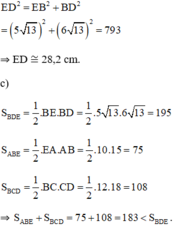

a) + ΔABE vuông tại A.
+ ΔBCD vuông tại C.
+ Ta có:
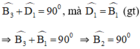
Vậy ΔBED vuông tại B.
b) + Áp dụng định lý Pytago trong ΔABE vuông tại A ta có:
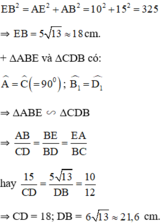
+ Áp dụng định lý Pytago trong ΔEBD vuông tại B ta có:
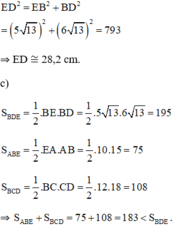

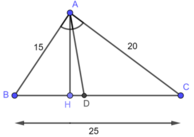
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
⇒\(\dfrac{DB}{DC}\)=\(\dfrac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\dfrac{DC}{DB}\)=\(\dfrac{15}{20}\)
⇒\(\dfrac{DB}{DB+DC}\)=\(\dfrac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
⇒\(\dfrac{DB}{BC}\)=\(\dfrac{15}{35}\)⇒DB=\(\dfrac{15}{35}\).BC=\(\dfrac{15}{35}\).25=\(\dfrac{75}{5}\)(cm)
b) Kẻ AH⊥BC
Ta có:\(S_{ABD}\)=\(\dfrac{1}{2}\)AH.BD
\(S_{ACD}\)=\(\dfrac{1}{2}\)AH.CD
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.CD}\)=\(\dfrac{BD}{DC}\)
Mà \(\dfrac{DB}{DC}\)=\(\dfrac{15}{12}\)=\(\dfrac{3}{4}\)
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{3}{4}\)(đpcm)

Hình tự vẽ lấy nhé
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
\(\Rightarrow\frac{DB}{DC}=\frac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\frac{DB}{DC}=\frac{15}{20}\)
\(\Rightarrow\frac{DB}{DB+DC}=\frac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
\(\Rightarrow\frac{DB}{BC}=\frac{15}{35}\Rightarrow DB=\frac{15}{35}.BC=\frac{15}{35}.25=\frac{75}{7}\left(cm\right)\)
b) Kẻ \(AH\perp BC\)
Ta có: \(S_{ABD}=\frac{1}{2}AH.BD\)
\(S_{ACD}=\frac{1}{2}AH.CD\)
\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.CD}=\frac{BD}{DC}\)
Mà \(\frac{DB}{DC}=\frac{15}{12}=\frac{3}{4}\)
\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{3}{4}\left(đpcm\right)\)

a) Xét tam giác ABC có:
BD là tia phân giác \(\widehat{BAC}\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{DC}=\dfrac{15}{20}=\dfrac{3}{4}\)(tính chất)
\(\Rightarrow\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{BC}{7}=\dfrac{25}{7}\)(tính chất dãy tỉ số bằng nhau)
\(\Rightarrow\left\{{}\begin{matrix}DB=\dfrac{25.3}{7}=\dfrac{75}{7}\left(cm\right)\\DC=\dfrac{25.4}{7}=\dfrac{100}{7}\left(cm\right)\end{matrix}\right.\)
b) Kẻ đường cao AH của tam giác ABC
\(\Rightarrow\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{\dfrac{1}{2}.AH.DC}{\dfrac{1}{2}.AH.BC}=\dfrac{DC}{BC}=\dfrac{100}{7}:25=\dfrac{4}{7}\)
a: Xét ΔABC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{15}=\dfrac{CD}{20}\)
mà BD+CD=25cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{15}=\dfrac{CD}{20}=\dfrac{25}{35}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{75}{7}cm;CD=\dfrac{100}{7}cm\)

a: BD/CD=12/16=3/4
=>S ABD/ SACD=3/4
b: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
AD là phân giác
=>BD/3=CD/4=20/7
=>BD=60/7cm; CD=80/7cm
\(AH=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\)

a: BC=căn 12^2+16^2=20cm
Xét ΔABC có AD là phân giác
nên BD/DC=AB/AC=3/4
=>BD/3=DC/4=(BD+DC)/(3+4)=20/7
=>BD=60/7cm; DC=80/7cm
Xét ΔCAB có ED//AB
nên ED/AB=CD/CB=4/7
=>ED/12=4/7
=>ED=48/7cm
b: S ABC=1/2*12*16=96cm2
BD/BC=3/7
=>S ABD/S ABC=3/7
=>S ABD=288/7cm2