Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi h là chiều cao của tam giác cân có đáy là a và cạnh bên là b.
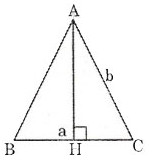
Theo định lý Pitago ta có
h2 = b2 -  =
= 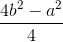
h = 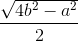
Nên S =  ah =
ah =  a.
a. 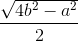 =
=  a.
a. 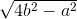 .
.

a:ΔSBC cân tại S có SM là trung tuyến
nên SM vuông góc BC
BC=6cm
=>BM=CM=3cm
SM=căn 5^2-3^2=4cm
Sxq=5*3/2*4=5*3*2=30cm2
Stp=30+5^2*căn 3/2=(60+25căn 3)/2cm2
b: BC vuông góc SM
BC vuông góc AM
=>BC vuông góc (SAM)

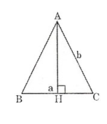
Gọi h là chiều cao của tam giác cân.
Theo định lí Pitago ta có:
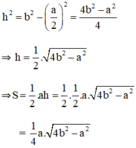

\(P=\dfrac{6+5+5}{2}=8\left(cm\right)\)
\(S=\sqrt{8\cdot\left(8-5\right)\cdot\left(8-5\right)\cdot\left(8-6\right)}=\sqrt{16\cdot9}=12\left(cm^2\right)\)

Gọi h là chiều cao của tam giác cân có đáy là a và cạnh bên là b.
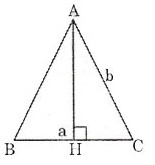
Theo định lý Pitago ta có
h2 = b2 –  =
= 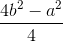
h = 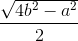
Nên S =  ah =
ah =  a.
a. 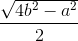 =
=  a.
a. 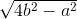
Tự vẽ hình nhé bạn
Gọi h là chiều cao của tam giác cân có đáy là a và cạnh bên là b.
Theo định lý Pitago ta có :
\(h^2=b^2-\left(\frac{a}{b}\right)^2=\frac{4b^2-a^2}{4}\)
\(h=\frac{\sqrt{4b^2-a^2}}{2}\)
\(\Rightarrow S=\frac{1}{2}ah=\frac{1}{2}a.\frac{\sqrt{4b^2-a^2}}{2}=\frac{1}{4}a.\sqrt{4b^2-a^2}\)

Gọi tam giác cần tìm là ABC cân tại A. Từ A kẻ AH vuông góc với BC.
=> BH=CH=\(\frac{6}{2}\)=3 (cm). theo định lí Py-ta-go => AH= 4cm
Vậy SABC= AH.BC.\(\frac{1}{2}\) = 4.6.\(\frac{1}{2}\)= 12 cm2
Bạn tự vẽ hình nhé
Từ A kẻ \(AH\perp BC\)
Xét \(\Delta ABC\) cân tại A có AH là đường cao (vì \(AH\perp BC\) )
=> AH đồng thời là đường trung tuyến
=> H là trung điểm của BC
=> BH = HC = \(\frac{6}{2}=3\left(cm\right)\)
Xét \(\Delta ABH\) vuông tại H có \(AH^2+BH^2=AB^2\) (định lí Py-ta-go)
<=> \(AH^2+3^2=5^2\)
<=> \(AH^2=25-9\)
<=> \(AH=4\) (vì \(AH\ge0\) )
Có \(S_{ABC}=\frac{1}{2}.6.4=12\left(cm^2\right)\)
Vậy diện tích của tam giác cân có đáy bằng 6cm và cạnh bên bằng 5cm là \(12cm^2\)
Chúc bạn học tốt :))