
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo t/c dãy tỉ số=nhau:
\(\frac{x^3+y^3}{6}=\frac{x^3-2y^3}{4}=\frac{2x^3+2y^3}{12}=\frac{2x^3+2y^3+x^3-2y^3}{12+4}=\frac{3x^3}{16}\) (hơi tắt tí)
và \(\frac{x^3+y^3}{6}=\frac{x^3-2y^3}{4}=\frac{x^3+y^3-\left(x^3-2y^3\right)^{ }}{6-4}=\frac{3y^3}{2}\)
Do đó \(\frac{3x^3}{16}=\frac{3y^3}{4}=>\frac{x^3}{8}=y^3=>\frac{x^6}{64}=y^6\)
\(=>\left(\frac{x^6}{64}\right).y^6=y^6.y^6=>\frac{x^6.y^6}{64}=y^{12}=\frac{64}{64}=1\)
=>y=1 hoặc y=-1
x=2 hoặc x=-2
Vậy....................
bạn ơi cho mik hs tại s ở trên là 3y^3/2 mak s ở dưới là 3x^3/16 = 3y^3/4 ?

Đáp án A. Theo quy luật : cứ sau vòng lặp 2 số (vd 7-8) thì số thứ nhất giảm đi 1 đơn vị (vd 7->6) và số thứ 2 tăng lên 1 đơn vị (vd 8->9)

vd câu 1:
ta có x-y=4 =>x=4+y
ta có pt:
4+y/y-2=3/2
=>8+2y=3y-6
=>-y=-14
=>y=14
=>x=4+y=4+14=18
các bài khác cũng tương tự thôi bạn

2) Ta có:
\(B=x^4+2x^3y-2x^3+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)
\(=x^4+x^3y-2x^3+x^3y+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)
\(=\left(x^4+x^3y-2x^3\right)+\left(x^3y+x^2y^2-2x^2y\right)-\left[x\left(x+y\right)-2x\right]+3\)
Do \(x+y-2=0\Rightarrow x+y=2\)
\(\Rightarrow B=\left(x^4+x^3y-2x^3\right)+\left(x^3y+x^2y^2-2x^2y\right)-\left[2x-2x\right]+3\)
\(=x^3.\left(x+y-2\right)+x^2y\left(x+y-2\right)-0+3\)
\(=0+0+3\)
\(=3\)
Vậy \(B=3\)
1) Ta có:
\(A=x^3+x^2y-2x^2-xy-y^2+3y+x-1\)
\(=\left(x^3+x^2y-2x^2\right)-\left(xy+y^2-2y\right)+y+x-1\)
\(=x^2\left(x+y-2\right)-y\left(x+y-2\right)+\left(x+y-2\right)+1\)
\(=0+0+0+1\)
\(=1\)
Vậy \(A=1\)

b: \(\Leftrightarrow\left(3x-1\right)^2=25\)
\(\Leftrightarrow3x-1\in\left\{5;-5\right\}\)
hay \(x\in\left\{2;-\dfrac{4}{3}\right\}\)
c: \(\Leftrightarrow\left(2x-5\right)^3=-81\)
\(\Leftrightarrow2x-5=-3\sqrt[3]{3}\)
hay \(x=\dfrac{5-\sqrt[3]{3}}{2}\)
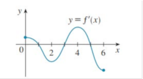


 bit lm bài này k giup tui
bit lm bài này k giup tui
Đáp án B
Ta có y = x 7 6 = x 7 / 6 ⇒ y ' = 7 6 x 1 / 6 = 7 6 x 6 .
Chọn phương án B