Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Tập xác định : D = R { 1 }.
> 0, ∀x
1.
Hàm số đồng biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
b) Tập xác định : D = R { 1 }.
< 0, ∀x
1.
Hàm số nghịch biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
c) Tập xác định : D = (-∞ ; -4] ∪ [5 ; +∞).
∀x ∈ (-∞ ; -4] ∪ [5 ; +∞).
Với x ∈ (-∞ ; -4) thì y’ < 0; với x ∈ (5 ; +∞) thì y’ > 0. Vậy hàm số nghịch biến trên khoảng (-∞ ; -4) và đồng biến trên khoảng (5 ; +∞).
d) Tập xác định : D = R { -3 ; 3 }.
< 0, ∀x
±3.
Hàm số nghịch biến trên các khoảng : (-∞ ; -3), (-3 ; 3), (3 ; +∞).
Lời giải:
Đặt \(\log_yx=a,\log_xy=b\). Khi đó ta có:
\(\left\{\begin{matrix} a+b=\frac{10}{3}\\ ab=\log_xy.\log_yx=1\end{matrix}\right.\)
Áp dụng định lý Viete đảo thì \(a,b\) là nghiệm của PT:
\(x^2-\frac{10}{3}x+1=0\) . PT trên có hai nghiệm \(3,\frac{1}{3}\)
Giả sử \(a=\log_yx=3\) và \(b=\log_xy=\frac{1}{3}\)
\(\left\{\begin{matrix} \log_y\left(\frac{144}{y}\right)=3\\ \log_x\left(\frac{144}{x}\right)=\frac{1}{3} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x=24\sqrt{3}\\ y=2\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow \frac{x+y}{2}=13\sqrt{3}\). Đáp án D
a) Vì .png)
và .png)
( hoặc .png)
và .png)
) nên các đường thẳng: x = -3 và x = 3 là các tiệm cận đứng của đồ thị hàm số.
Vì .png)
và .png)
nên các đường thẳng: y = 0 là các tiệm cận ngang của đồ thị hàm số.
b) Hai tiệm cận đứng : .png)
; tiệm cận ngang : .png)
.
c) Tiệm cận đứng : x = -1 ;
vì .png)
nên đồ thị hàm số không có tiệm cận ngang.
d) Hàm số xác định khi : .png)
Vì .png)
( hoặc .png)
) nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
Vì .png)
nên đường thẳng y = 1 là tiệm cận ngang (về bên phải) của đồ thị hàm số.
Bạn kiểm tra lại đề. Và vào hoc 24 để đăng nhé!
Làm câu cuối:
TXĐ: \(x\in\)[ 0 ; + vô cùng )
\(y'=\frac{1}{2\sqrt{x}}-1=0\Leftrightarrow2\sqrt{x}=1\Leftrightarrow x=\frac{1}{4}\left(tm\right)\)
Vẽ bảng biến thiên:
....
Từ bảng biên thiên:
Hàm số đồng biến trong khoảng ( 0 ; 1/4 )
Hàm số nghịch biên trong khoảng ( 1/4 ; + dương vô cùng)
a) y′=6x2+6x−36=6(x2+x−6)y′=6x2+6x−36=6(x2+x−6)
y’= 0 ⇔ x2+ x – 6= 0 ⇔ x=2; x=-3
Bảng biến thiên :
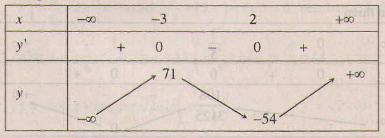
Hàm số đạt cực đại tại x = -3 , ycđ = y(-3) = 71
Hàm số đạt cực tiểu tại x = 2 , y(ct) = y(2) = -54
b) y’ = 4x3 + 4x = 4x(x2 + 1); y’ = 0 ⇔ x = 0.
Bảng biến thiên :
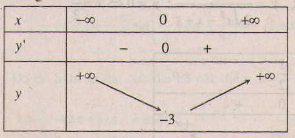
Hàm số đạt cực tiểu tại x = 0 , y(ct) = y(0) = -3
c) Tập xác định : D = R\{0}
Bảng biến thiên :
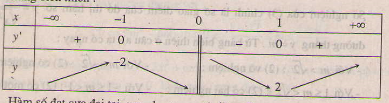
Hàm số đạt cực đại tại x = -1 , ycđ = y(-1) = -2 ;
Hàm số đạt cực tiểu tại x = 1 , yct = y(1) = 2.
d) Tập xác định : D = R.
y’ = 3x2(1 – x)2 + x3 . 2(1 – x)(-1) = x2 (1 – x)[3(1 – x) - 2x] = x2 (x – 1)(5x – 3) .
y’ = 0 ⇔ x = 0, x =
, x = 1.
Bảng biến thiên :
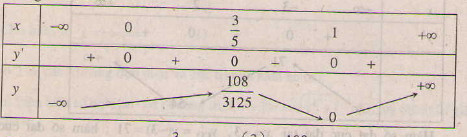
Hàm số đạt cực đại tại x = , ycđ = 
= 
;
Hàm số đạt cực tiểu tại x = 1 , yct = y(1) = 0 .
e) Tập xác định : D = R. 
Hàm số đạt cực tiểu tại 
a) Tập xác định : R\ {1}; y′=−4(x−1)2<0,∀x≠1y′=−4(x−1)2<0,∀x≠1 ;
Tiệm cận đứng : x = 1 . Tiệm cận ngang : y = 1.
Bảng biến thiên :
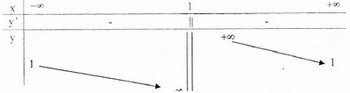
Đồ thị như hình bên.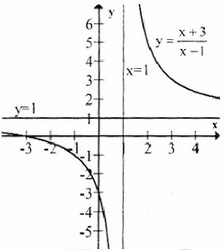 
b) Tập xác định : R \{2}; y′=6(2x−4)2>0,∀x≠2y′=6(2x−4)2>0,∀x≠2
Tiệm cận đứng : x = 2 . Tiệm cận ngang : y = -1.
Bảng biến thiên :
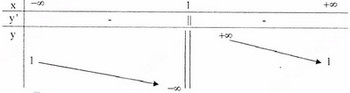
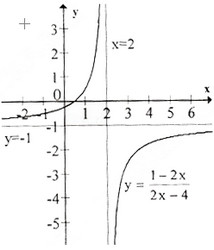
Đồ thị như hình bên.
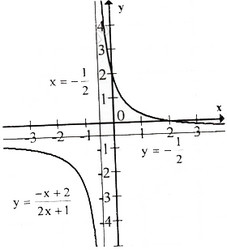
c) Tập xác định : R∖{−12}R∖{−12}; y′=−5(2x+1)2<0,∀x≠−12y′=−5(2x+1)2<0,∀x≠−12
Tiệm cận đứng : x=−12x=−12 . Tiệm cận ngang : y=−12y=−12.
Bảng biến thiên :
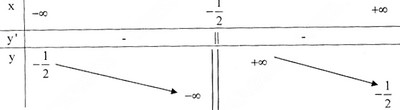
Đồ thị như hình bên.
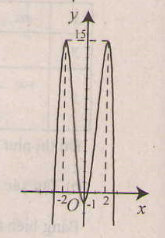
a) Tập xác định : R ; y' =-4x3 + 16x = -4x(x2 - 4);
y' = 0 ⇔ x = 0, x = ±2 .
Bảng biến thiên :
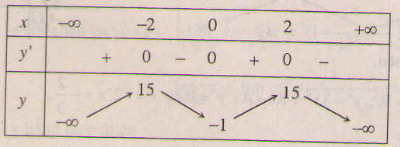
Đồ thị như hình bên.
b) Tập xác định : R ; y' =4x3 - 4x = 4x(x2 - 1);
y' = 0 ⇔ x = 0, x = ±1 .
Bảng biến thiên :
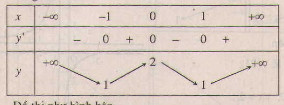
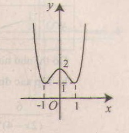
Đồ thị như hình bên.
c) Tập xác định : R ; y' =2x3 + 2x = 2x(x2 + 1); y' = 0 ⇔ x = 0.
Bảng biến thiên :
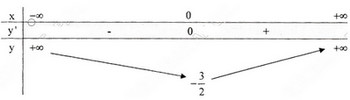
Đồ thị như hình bên.
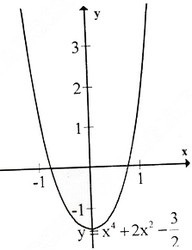
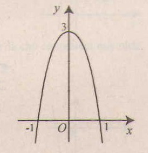
d) Tập xác định : R ; y' = -4x - 4x3 = -4x(1 + x2); y' = 0 ⇔ x = 0.
Bảng biến thiên :
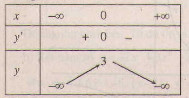
Đồ thị như hình bên.
.
a) Vì .png)
( hoặc .png)
) nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
Vì .png)
( hoặc .png)
) nên đường thẳng y = -1 là tiệm cận ngang của đồ thị hàm số.
b) Tiệm cận đứng : x = -1 ; tiệm cận ngang : y = -1.
c) Tiệm cận đứng : .png)
; tiệm cận ngang :
d) Tiệm cận đứng : x = 0 ; tiệm cận ngang : y = -1.
a: \(y=\left(2x^2-x+1\right)^{\dfrac{1}{3}}\)
=>\(y'=\dfrac{1}{3}\left(2x^2-x+1\right)^{\dfrac{1}{3}-1}\cdot\left(2x^2-x+1\right)'\)
\(=\dfrac{1}{3}\cdot\left(4x-1\right)\left(2x^2-x+1\right)^{-\dfrac{2}{3}}\)
b: \(y=\left(3x+1\right)^{\Omega}\)
=>\(y'=\Omega\cdot\left(3x+1\right)'\cdot\left(3x+1\right)^{\Omega-1}\)
=>\(y'=3\Omega\left(3x+1\right)^{\Omega-1}\)
c: \(y=\sqrt[3]{\dfrac{1}{x-1}}\)
=>\(y'=\dfrac{\left(\dfrac{1}{x-1}\right)'}{3\cdot\sqrt[3]{\left(\dfrac{1}{x-1}\right)^2}}\)
\(=\dfrac{\dfrac{1'\left(x-1\right)-\left(x-1\right)'\cdot1}{\left(x-1\right)^2}}{\dfrac{3}{\sqrt[3]{\left(x-1\right)^2}}}\)
\(=\dfrac{-x}{\left(x-1\right)^2}\cdot\dfrac{\sqrt[3]{\left(x-1\right)^2}}{3}\)
\(=\dfrac{-x}{\sqrt[3]{\left(x-1\right)^4}\cdot3}\)
d: \(y=log_3\left(\dfrac{x+1}{x-1}\right)\)
\(\Leftrightarrow y'=\dfrac{\left(\dfrac{x+1}{x-1}\right)'}{\dfrac{x+1}{x-1}\cdot ln3}\)
\(\Leftrightarrow y'=\dfrac{\left(x+1\right)'\left(x-1\right)-\left(x+1\right)\left(x-1\right)'}{\left(x-1\right)^2}:\dfrac{ln3\left(x+1\right)}{x-1}\)
\(\Leftrightarrow y'=\dfrac{x-1-x-1}{\left(x-1\right)^2}\cdot\dfrac{x-1}{ln3\cdot\left(x+1\right)}\)
\(\Leftrightarrow y'=\dfrac{-2}{\left(x-1\right)\cdot\left(x+1\right)\cdot ln3}\)
e: \(y=3^{x^2}\)
=>\(y'=\left(x^2\right)'\cdot ln3\cdot3^{x^2}=2x\cdot ln3\cdot3^{x^2}\)
f: \(y=\left(\dfrac{1}{2}\right)^{x^2-1}\)
=>\(y'=\left(x^2-1\right)'\cdot ln\left(\dfrac{1}{2}\right)\cdot\left(\dfrac{1}{2}\right)^{x^2-1}=2x\cdot ln\left(\dfrac{1}{2}\right)\cdot\left(\dfrac{1}{2}\right)^{x^2-1}\)
h: \(y=\left(x+1\right)\cdot e^{cosx}\)
=>\(y'=\left(x+1\right)'\cdot e^{cosx}+\left(x+1\right)\cdot\left(e^{cosx}\right)'\)
=>\(y'=e^{cosx}+\left(x+1\right)\cdot\left(cosx\right)'\cdot e^u\)
\(=e^{cosx}+\left(x+1\right)\cdot\left(-sinx\right)\cdot e^u\)
a) \(y=\left(2x^2-x+1\right)^{\dfrac{1}{3}}\)
\(\Rightarrow y'=\dfrac{1}{3}.\left(2x^2-x+1\right)^{\dfrac{1}{3}-1}.\left(4x-1\right)\)
\(\Rightarrow y'=\dfrac{1}{3}.\left(2x^2-x+1\right)^{-\dfrac{2}{3}}.\left(4x-1\right)\)
b) \(y=\left(3x+1\right)^{\pi}\)
\(\Rightarrow y'=\pi.\left(3x+1\right)^{\pi-1}.3=3\pi.\left(3x+1\right)^{\pi-1}\)
c) \(y=\sqrt[3]{\dfrac{1}{x-1}}\)
\(\Rightarrow y'=\dfrac{\left(x-1\right)^{-1-1}}{3\sqrt[3]{\left(\dfrac{1}{x-1}\right)^{3-1}}}=\dfrac{\left(x-1\right)^{-2}}{3\sqrt[3]{\left(\dfrac{1}{x-1}\right)^2}}=\dfrac{1}{3.\sqrt[]{x-1}.\sqrt[3]{\left(\dfrac{1}{x-1}\right)^2}}\)
\(\Rightarrow y'=\dfrac{1}{3\left(x-1\right)^{\dfrac{1}{2}}.\left(x-1\right)^{\dfrac{2}{3}}}=\dfrac{1}{3\left(x-1\right)^{\dfrac{7}{6}}}=\dfrac{1}{3\sqrt[6]{\left(x-1\right)^7}}\)
d) \(y=\log_3\left(\dfrac{x+1}{x-1}\right)\)
\(\Rightarrow y'=\dfrac{\dfrac{1-\left(-1\right)}{\left(x-1\right)^2}}{\dfrac{x+1}{x-1}.\ln3}=\dfrac{2}{\left(x+1\right)\left(x-1\right).\ln3}\)
e) \(y=3^{x^2}\)
\(\Rightarrow y'=3^{x^2}.ln3.2x=2x.3^{x^2}.ln3\)
f) \(y=\left(\dfrac{1}{2}\right)^{x^2-1}\)
\(\Rightarrow y'=\left(\dfrac{1}{2}\right)^{x^2-1}.ln\dfrac{1}{2}.2x=2x.\left(\dfrac{1}{2}\right)^{x^2-1}.ln\dfrac{1}{2}\)
Các bài còn lại bạn tự làm nhé!