QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
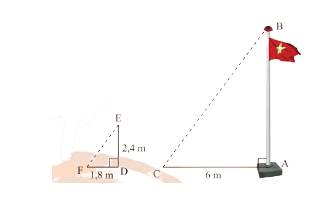
Cùng một thời điểm thì góc tạo bởi tia nắng và mặt đất là như nhau. Do đó, \(\widehat {EFD} = \widehat {BCA}\).
Xét tam giác \(DEF\) và tam giác \(ABC\) ta có:
\(\widehat {EFD} = \widehat {BCA}\) (chứng minh trên)
\(\widehat {EDF} = \widehat {BAC} = 90^\circ \).
Do đó, \(\Delta DEF\backsim\Delta ABC\) (g.g)
Suy ra, \(\frac{{FD}}{{AC}} = \frac{{ED}}{{AB}} \Leftrightarrow \frac{{1,8}}{6} = \frac{{2,4}}{{AB}} \Rightarrow AB = \frac{{6.2,4}}{{1,8}} = 8\).
Vậy cột cờ \(AB\) cao 8m.
23 tháng 7 2023
`a,`
| Hoạt động | Tại chỗ | Vận động |
| Số học sinh | 28 | 14 |
Số học sinh tham gia hoạt động tại chỗ gấp `28 : 14 = 2` lần hoạt động vận động.
`b,` Lớp nên tăng cường vận động.
QT
2
13 tháng 9 2023
Xét ΔABC có D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình
=>DE=1/2BC
=>BC=2DE=90(m)
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
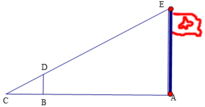
Vì \(BD = DA \Rightarrow D\) là trung điểm của \(AB\);
Vì \(EC = EA \Rightarrow E\) là trung điểm của \(AC\).
Do đó, \(DE\) là đường trung bình của tam giác \(ABC\)
\( \Rightarrow \left\{ \begin{array}{l}DE//BC\\DE = \frac{1}{2}BC\end{array} \right.\) (tính chất đường trung bình).
\( \Rightarrow 45 = \frac{1}{2}BC \Leftrightarrow BC = 45.2 = 90\left( m \right)\)
Vậy khoảng các của hai điểm \(B\) và \(C\) là 90 m.
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
a) Gọi x là độ cao của cột đèn, có: \(\frac{{0,6}}{3} = \frac{{1,4}}{x}\)
=> x = 7m
b) Gọi y là độ dài bóng cột cờ, có \(\frac{3}{y} = \frac{{1,4}}{7}\)
=> y = 15m
23 tháng 7 2023
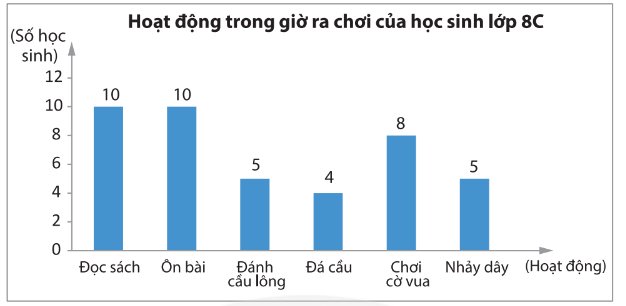
Số lượng học sinh đọc sách ko hợp lí vì tổng số học sinh sẽ ko đến mức 90 học sinh
Số học sinh nhảy dây cũng không hợp lí vì không đúng định dạng
Số học sinh ôn bài, chơi cầu lông, đá cầu, chơi cờ vua hợp lí
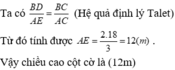
Cùng một thời điểm thì góc tạo bởi tia nắng và mặt đất là như nhau. Do đó, \(\widehat {EFD} = \widehat {BCA}\).
Xét tam giác \(DEF\) và tam giác \(ABC\) ta có:
\(\widehat {EFD} = \widehat {BCA}\) (chứng minh trên)
\(\widehat {EDF} = \widehat {BAC} = 90^\circ \).
Do đó, \(\Delta DEF\backsim\Delta ABC\) (g.g)
Suy ra, \(\frac{{FD}}{{AC}} = \frac{{ED}}{{AB}} \Leftrightarrow \frac{{1,8}}{6} = \frac{{2,4}}{{AB}} \Rightarrow AB = \frac{{6.2,4}}{{1,8}} = 8\).
Vậy cột cờ \(AB\) cao 8m.