
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\widehat{DAB}+\widehat{ADC}=180^0\)
mà \(\widehat{DAB}=3\widehat{ADC}\)\(\Rightarrow\widehat{ADC}=45^0\Rightarrow\widehat{DAB}=135^0\)
\(\widehat{ABC}+\widehat{BCD}=180^0\) mà lại có: \(\widehat{ABC}-\widehat{BCD}=30^0\)
\(\Rightarrow\widehat{BCD}=75^0\Rightarrow\widehat{ABC}=105^0\)

theo tính chất của hình thang thì tổng 2 góc kề 2 cạnh bên =180
theo đó: nếu AB,CD là 2 đáy hình thang thì
góc A+góc D=180 <=> D+3D=180 <=> 4D=180 <=> D=45 độ => A=3.45=135
góc B-C=30 => B=C+30
B+C=180<=> C+30+C=180 <=> 2C=150 <=> C=75 độ => B=75+30=105
cho mot hinh thang AB//CD biet B-C= 30 tinh cac goc con lai

Ta có
B + C = 180
MÀ : B - C = 30 => B= 30+C
=> 30 + C +C =180
=> 2C =180-30=150
=> C= 150: 2 =75
THAY C= 75 VÀO B+C =180
=> B+75=180
=> B=180-75
=>B=105
TA CÓ
A = 3D
MÀ A+ D = 180 => A= 180-D
=> 180 -3D=D
=> 180=3D+D=4D
=> 180:4=D
=> D=45
THAY D= 45 VÀO A=3D
=> A= 3.45
=>A=135
1 T i c k nha
________ CHÚC BẠN HỌC TỐT_____________

*Ta có: A=2D (1)
A+D=180 (2)
Thay (1) vào (2) ta đươc:
A+D=180\(\Rightarrow\)2D+D=180\(\Rightarrow\)3D=180
\(\Rightarrow\)D=\(\frac{180}{3}\)=60\(\Rightarrow\)A=2D=2*60=120
*Ta có: B+C=180 (1)
MÀ B-C=20\(\Rightarrow\)B=20+C (2)
Thay (1) vào (2) \(\Rightarrow\)B+C=180
\(\Rightarrow\)20+C+C=180
\(\Rightarrow\)20+2D=180
\(\Rightarrow\)2D=180-20
\(\Rightarrow\)2D=160
\(\Rightarrow\)D=\(\frac{160}{2}=80\)

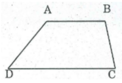
Ta có: hình thang ABCD có AB // CD ⇒ ∠ A + ∠ D = 180 0 (hai góc trong cùng phía)
Ta có: ∠ A = 3 ∠ D (gt)
⇒ 3 ∠ D + ∠ D = 180 0 ⇒ 4 ∠ D = 180 0 ⇒ ∠ D = 45 0 ⇒ ∠ A = 3. 45 0 = 135 0
∠ B + ∠ C = 180 0 (hai góc trong cùng phía)
∠ B - ∠ C = 30 0 (gt)
⇒ 2 ∠ B = 180 0 + 30 0 = 210 0 ⇒ ∠ B = 105 0
∠ C = ∠ B - 30 0 = 105 0 – 30 0 = 75 0

Ta có:
Xét hình thang ABCD(AB//CD) ta có:
\(\widehat{A}+\widehat{D}=\widehat{B}+\widehat{C}=180^0\)
Mà \(\left\{{}\begin{matrix}\widehat{A}=3\widehat{D}\\\widehat{B}-\widehat{C}=30^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3\widehat{D}+\widehat{D}=180^0\\30^0+\widehat{C}+\widehat{C}=180^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{D}=45^0\\\widehat{C}=75^0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\widehat{A}=135^0\\\widehat{B}=105^0\end{matrix}\right.\)
Vậy...