LL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
0
T
11 tháng 7 2019
#)Giải :
A B C H
Áp dụng định lí Py - ta - go :
\(BC^2=AB^2+AC^2\Leftrightarrow BC^2=3^2+4^2=9+16=25\)
\(\Rightarrow BC=\sqrt{25}=5\)
Ta có : \(AB.AC=BC.AH\)
\(\Rightarrow3.4=5.AH\Rightarrow H=\frac{12}{5}\)
\(\hept{\begin{cases}AB^2=BC.BH\Rightarrow BH=\frac{AB^2}{BC}=\frac{3^2}{5}=\frac{9}{5}\\AC^2=BC.CH\Rightarrow CH=\frac{AC^2}{BC}=\frac{4^2}{5}=\frac{16}{5}\end{cases}}\)
Vậy \(\hept{\begin{cases}BC=5\\BH=\frac{9}{15}\\CH=\frac{16}{5}\end{cases}}\)
CM
26 tháng 12 2017
Xét hai tam giác vuông DAC và DBA ,ta có:
∠ (ADC) = ∠ (BDA) = 90 0
∠ C = ∠ (DAB) (hai góc cùng phụ ∠ B )
Suy ra: △ DAC đồng dạng △ DBA (g.g)
Suy ra: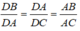 
⇒ D A 2 = D B . D C
hay DA = D B . D C = 9 . 16 = 12 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:
A B 2 = D A 2 + D B 2 = 9 2 + 12 2 = 225 ⇒ AB =15 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACD,ta có:
AC2 = DA2 + DC2 = 122 +162 = 400 ⇒ AC = 20cm
Vậy BC = BD + DC = 9 + 16 = 25(cm)
26 tháng 6 2017
Gọi độ dài ba cạnh của tam giác là a, b, c (cm) ( Điều kiện : a,b,c>0)
Ta có: \(S=\frac{1}{2}.12a=\frac{1}{2}.15b=\frac{1}{2}.20c\)
\(\Leftrightarrow12a=15b=20b\)
\(\Leftrightarrow\frac{a}{\frac{1}{12}}=\frac{b}{\frac{1}{15}}=\frac{c}{\frac{1}{20}}\)
ÁP DỤNG TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU TA CÓ:
\(\frac{a}{\frac{1}{12}}=\frac{b}{\frac{1}{15}}=\frac{c}{\frac{1}{20}}=\frac{a+b+c}{\frac{1}{12}+\frac{1}{15}+\frac{1}{20}}=\frac{60}{\frac{1}{5}}=60.5=300\)
\(\Leftrightarrow\hept{\begin{cases}\frac{a}{\frac{1}{12}}=300\\\frac{b}{\frac{1}{15}}=300\\\frac{c}{\frac{1}{20}}=300\end{cases}\Leftrightarrow\hept{\begin{cases}a=300.\frac{1}{12}\\b=300.\frac{1}{15}\\c=300.\frac{1}{20}\end{cases}\Leftrightarrow}\hept{\begin{cases}a=25\left(cm\right)\\b=20\left(cm\right)\\c=15\left(cm\right)\end{cases}}}\)
Vậy độ dài ba cạnh của tam giác là 25cm, 20cm, 15cm
26 tháng 6 2017
Gọi 3 cạnh của tam giác có độ dài là x, y, z
=> x+y+z=60x+y+z=60
Như ta đã học, diện tích tam giác =1/2.h.a
Trong đó a là một cạnh của tam giác; h là chiều cao hạ từ một đỉnh lên cạnh a
Áp dụng vào bài này ta có: 1/2.12.x=1/2.15.y=1/2.20.z
Vì bài này 3 cạnh có thể coi như nhau, nên có thể hoán đổi vị trí của chúng
Rút ra thay vào, ta được tam giác thỏa mãn yêu cầu bài toán có 3 cạnh là 36cm;2,4cm;21,6cm
31 tháng 8 2023
4:
a: Gọi độ dài cạnh góc vuông cần tìm là x
Theo đề, ta có: x^2+x^2=a^2
=>2x^2=a^2
=>x^2=a^2/2=2a^2/4
=>\(x=\dfrac{a\sqrt{2}}{2}\)
b:
Độ dài cạnh là;
\(h:\dfrac{\sqrt{3}}{2}=\dfrac{2h}{\sqrt{3}}\)
5:
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>13^2=12^2+HB^2
=>HB=5cm
BC=5+16=21cm
ΔAHC vuông tại H
=>AH^2+HC^2=AC^2
=>AC^2=16^2+12^2=400
=>AC=20(cm)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
4 tháng 9 2023
Cảm ơn em câu hỏi của em thật là thù vị. Về thắc mắc của em cô nghĩ chắc cũng có nhiều bạn đang muốn biết lắm ý nhỉ? Về vấn đề em hỏi cô xin trả lời như sau:
Tình theo a ở đây không phải là a mà mình tùy chọn em nhá. a ở đây là một ẩn a, em cứ tính độ dài của tam giác đó theo ẩn a thôi em ạ!
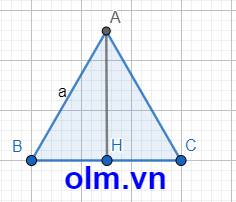
Vì ABC là tam giác đều nên đường cao cũng là đường trung tuyến của tam giác. Gọi AH là đường cao của tam giác thì
BH = HC = \(\dfrac{1}{2}\)a
Xét tam giác ACH vuông tại H. Theo pytago ta có:
AC2 = AH2 + HC2
⇒ AH2 = AC2 - HC2
⇒AH2 = a2 - (\(\dfrac{1}{2}\)a)2 = \(\dfrac{3}{4}\)a2
⇒ AH = \(\sqrt{\dfrac{3}{4}a^2}\) = \(\dfrac{3\sqrt{a}}{2}\)
(cân tại A) vẽ đường cao AH, đường cao BK
Hãy tính độ dài các cạnh của tam giác ABC
và BK, hãy tìm điều kiện của tam giác ABC để tam giác 
là tam giác đều ?
NL
19 tháng 2 2021
a) Vì \(\Delta ABC\) cân tại A, có AH là đường cao
\(\Rightarrow AH\) vừa là đường cao, vừa là đường phân giác của \(\Delta ABC\)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}=\dfrac{\widehat{A}}{2}\)
Xét \(\Delta ABH\) và \(\Delta ACH\) có:
\(\widehat{BAH}=\widehat{CAH}\left(cmt\right)\)
\(\widehat{AHB}=\widehat{AHC}=90^0\)
\(AH\): cạnh chung
\(\Rightarrow\Delta ABH=\Delta ACH\left(ch-gn\right)\)
Bạn học casio à, mình nhớ là bỏ thi rồi mà, chứ toán 8 nâng cao làm gì có mấy cái này, nếu mà muốn làm bài của bạn thì phải dùng các hàm số lượng giác, mà đó là toán 9 rồi :)