

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

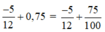


\(C=\left[-45^{10}.\left(-5\right)^{10}\right]:75^{10}\)
\(C=\left(-45^{10}.5^{10}\right):75^{10}\)
\(C=\left(-45.5\right)^{10}:75^{10}\)
\(C=\left(-225\right)^{10}:75^{10}\)
\(C=\left(-225:75\right)^{10}=\left(-3\right)^{10}=3^{10}\)
\(B=\left(7^4-7^3\right)^3:343^{12}\)
\(B=\left[7^3.\left(7-1\right)\right]^3:\left(7^3\right)^{12}\)
\(B=\left(7^3.6\right)^3:7^{36}\)
\(B=7^9.6^3:7^{36}\)
\(B=6^3:7^{27}\)

a)\(\frac{7}{12}.\frac{6}{11}+\frac{7}{12}.\frac{5}{11}-2\frac{7}{12}\)
\(=\frac{7}{12}.\left(\frac{6}{11}+\frac{5}{11}\right)-\frac{31}{12}\)
\(=\frac{7}{12}-\frac{31}{12}\)
\(=-2\)
b)\(\frac{-5}{9}.\frac{-6}{13}+\frac{5}{-9}.\frac{-5}{13}-\frac{5}{9}\)
\(=\frac{5}{9}.\left(\frac{6}{13}+\frac{5}{13}-1\right)\)
\(=\frac{5}{9}.\left(\frac{11}{13}-\frac{13}{13}\right)\)
\(=\frac{5}{9}.\frac{-2}{13}\)
\(=-\frac{10}{117}\)
c)\(0,8.\frac{-15}{14}-\frac{4}{5}.\frac{13}{14}-1\frac{2}{5}\)
\(=\frac{4}{5}.\frac{-15}{14}-\frac{4}{5}.\frac{13}{14}-\frac{7}{5}\)
\(=\frac{4}{5}.\left(-\frac{15}{14}-\frac{13}{14}\right)-\frac{7}{5}\)
\(=\frac{4}{5}.\left(-2\right)-\frac{7}{5}\)
\(=\frac{-8}{5}-\frac{7}{5}\)
\(=-3\)
d)\(-75\%.\frac{6}{7}+5\%.\frac{6}{7}+\frac{7}{10}.1\frac{1}{7}\)
\(=\frac{-15}{20}.\frac{6}{7}+\frac{1}{20}.\frac{6}{7}+\frac{7}{10}.\frac{8}{7}\)
\(=\frac{6}{7}.\left(\frac{-15}{20}+\frac{1}{20}\right)+\frac{4}{5}\)
\(=\frac{6}{7}.\frac{-7}{10}+\frac{4}{5}\)
\(=-\frac{3}{5}+\frac{4}{5}\)
\(=\frac{1}{5}\)
Linz

a) Ta có : \(45^{10}=5^{10}.3^{20}\)
\(\Rightarrow45^{10}.5^{30}=3^{20}.5^{10}.5^{30}=3^{20}.5^{40}=3^{20}.\left(5^2\right)^{20}=3^{20}.25^{20}=\left(3.25\right)^{20}=75^{20}\)
Vậy \(45^{10}.5^{30}=75^{20}\)
b) Ta có : \(12^8=3^8.2^{16}\)và \(9^{12}=3^{24}\)
\(\Rightarrow12^8.9^{12}=3^8.2^{16}.3^{24}=2^{16}.\left(3^2\right)^{16}=2^{16}.9^{16}=\left(2.9\right)^{16}=18^{16}\)
Vậy \(12^8.9^{12}=18^{16}\)

\(\frac{5}{12}-\left|-12\right|-4\cdot\sqrt{\frac{25}{16}}+2015^0\)
\(=\frac{5}{12}-12-4\cdot\frac{5}{4}+1\)
\(=\frac{5}{12}-\frac{144}{12}-\frac{60}{12}+\frac{12}{12}\)
\(=\frac{5-144-60+12}{12}\)
\(=\frac{-187}{12}\)

\(A=3\cdot\left(\dfrac{5}{9}+\dfrac{14}{99}\right):\left(\dfrac{8}{99}-\dfrac{4}{33}\right)\)
\(=3\cdot\dfrac{55+14}{99}:\dfrac{8-12}{99}\)
\(=3\cdot\dfrac{69}{-4}=\dfrac{-207}{4}\)

a) 128 . 912 = ( 3 . 22 )8 . ( 32 )12
= 38 . 216 . 324 = 332 . 216 = ( 32 )16 . 216 = ( 32 . 2 )16 = 1816
b) 4510 . 530 = 4510 . ( 53 )10
= ( 45 . 53 )10 = 562510
Mà 7520 = ( 752 )10 = 562510
Vậy 4510 . 530 = 7520

( x - \(\sqrt{3}\) )\(^{2016}\) \(\ge\) 0 với mọi x . Kí hiệu là 1
(y\(^2\) - 3 )\(^{2018}\)\(\ge\) 0 với mọi y . Kí hiệu là 2
Từ 1 và 2 suy ra ( x - \(\sqrt{3}\) )\(^{2016}\) = 0 và (y\(^2\) - 3 )\(^{2018}\) = 0 . Kí hiệu là 3
Từ 3 suy ra x - \(\sqrt{3}\) = 0 suy ra x = \(\sqrt{3}\)
y\(^2\)- 3 = 0 suy ra y\(^2\) = 0 suy ra y =..........
2. Trên tử đặt 3 ra ngoài. Dưới mẫu đặt 11 ra ngoài rồi triệt tiêu.
3. 17^18 = (17^3)^6 = 4913^6
63^12 = (63^2)^6 = 3969 ^6
Vì 4913 > 3969 nên 4913^6 > 3969^6 hay 17^18>63^12

Vì \(\Delta ABC=\Delta DEF\) nên \(\widehat{A}\) = \(\widehat{D}\) = \(55^o\)
Ta có : \(\widehat{D}\) + \(\widehat{E}\) + \(\widehat{F}\) = \(180^o\)
\(\widehat{F}\) = \(180^o\) - \(\widehat{D}\) - \(\widehat{E}\)
\(\widehat{F}\) = \(180^o\)- \(55^o\) - \(75^o\)
\(\widehat{F}\) = \(50^o\)
Vì \(\Delta ABC=\Delta DEF\) nên \(\widehat{B}\) = \(\widehat{E}\) = \(75^o\)

a) \(12^8.9^{12}=18^{16}\)
ta cóvế trái : \(12^8.9^{12}=\left(2^2.3\right)^8.\left(3^2\right)^{12}=2^{16}.3^8.3^{24}=2^{16}.3^{32}\)
vế phải :\(18^{16}=\left(2.3^2\right)^{16}=2^{16}.3^{32}\)
=> VT =VP
b) \(75^{20}=45^{10}.5^{30}\)
VT=\(75^{20}=\left(3.5^2\right)^{20}=3^{20}.5^{40}\)
VP = \(45^{10}.5^{30}=\left(2^2.5\right)^{10}.5^{30}=2^{20}.5^{30}\)
ta tháy VT=VP
=> ĐPCM