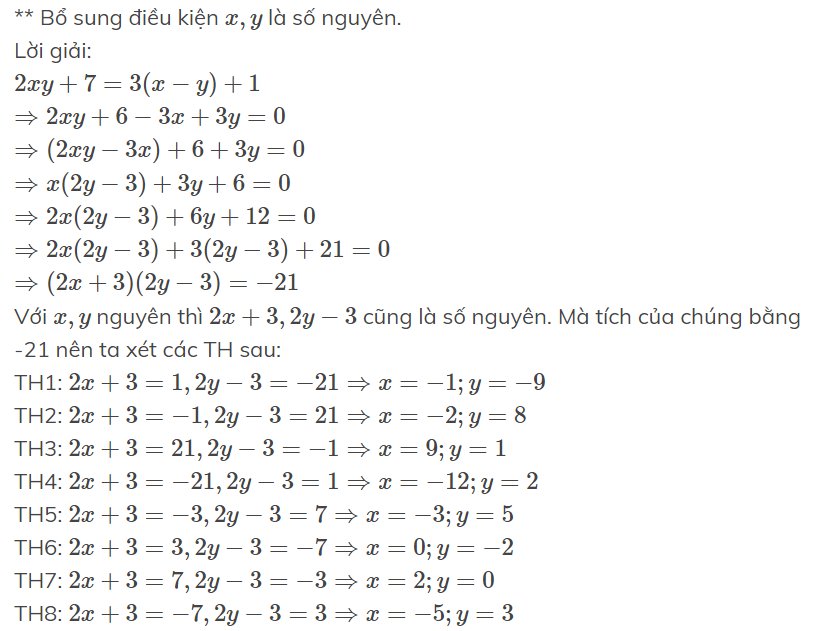K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NL
1
AH
Akai Haruma
Giáo viên
29 tháng 6 2024
** Bổ sung điều kiện $x,y$ là số nguyên.
Lời giải:
$2xy+7=3(x-y)+1$
$\Rightarrow 2xy+6-3x+3y=0$
$\Rightarrow (2xy-3x)+6+3y=0$
$\Rightarrow x(2y-3)+3y+6=0$
$\Rightarrow 2x(2y-3)+6y+12=0$
$\Rightarrow 2x(2y-3)+3(2y-3)+21=0$
$\Rightarrow (2x+3)(2y-3)=-21$
Với $x,y$ nguyên thì $2x+3, 2y-3$ cũng là số nguyên. Mà tích của chúng bằng -21 nên ta xét các TH sau:
TH1: $2x+3=1, 2y-3=-21\Rightarrow x=-1; y=-9$
TH2: $2x+3=-1, 2y-3=21\Rightarrow x=-2; y=8$
TH3: $2x+3=21, 2y-3=-1\Rightarrow x=9; y=1$
TH4: $2x+3=-21, 2y-3=1\Rightarrow x=-12; y=2$
TH5: $2x+3=-3, 2y-3=7\Rightarrow x=-3; y=5$
TH6: $2x+3=3, 2y-3=-7\Rightarrow x=0; y=-2$
TH7: $2x+3=7, 2y-3=-3\Rightarrow x=2; y=0$
TH8: $2x+3=-7, 2y-3=3\Rightarrow x=-5; y=3$
ND
0
S
20 tháng 9 2018
a) Ta có : x + 2xy + y = 7
=>2x + 4xy + 2y = 14
=>2x(1+2y) + 2y + 1 = 14 + 1
=>2x(2y+1) + 2y + 1 = 15
=>(2y+1).(2x+1) = 15
Giả sử x > y=> 2y+1 > 2x +1
Lập bảng là gia thôi!
b)Ta có : 2^x + 2^y =1025
TH1: 2^x lẻ, 2^y chẵn
=> 2^x lẻ=>2^x=1 => x= 1
Khi đó : 2^x + 2^y = 1025
=>1 +2^y = 1025
=> 2^y = 1024
=> 2^y = 2^10
=> y = 10
Vậy x = 1, y = 10
TH2: làm tương tự xét: 2^x chẵn , 2^y lẻ thì dc x= 10 , y= 1
TN
1
NT
29 tháng 10 2016
\(7-2xy=5y-8x\\ \Rightarrow7-2xy-5y-8x=0\\ \Rightarrow7=2xy+5y+8x\\ \Rightarrow7=2xy+8x+5y\\ \Rightarrow2x\left(y+4\right)+5\left(y+4\right)=37\)
\(\Rightarrow\left(y+4\right)\left(2x+5\right)=37\)
| 2x+5 | 1 | 37 | -1 | -37 |
| y+4 | 37 | 1 | -37 | -1 |
| x | -2 | 16 | -3 | -21 |
| y | 33 | -3 | -41 | -5 |
Vậy (x;y)=(-2;33);(16;-3);(-3;41);(-21;-5)
MY
1
VV
8 tháng 3 2023
a)ta có :2xy-6=4x-y => 2xy-6-4x+y=0 => 2*(2xy-6-4x+y)=2*0 =>4xy-12-8x+2y=0 => 2x2y-4-8-8x+2y=0 => 2x2y-4-8x+2y=8 =>(2x2y+2y)-(8x+4)=8 =>2y(2x+1)-4(2x+1)=8 => (2y-4)(2x+1)=8 Ta có bảng sau :
| 2y-4 | 1 | 8 | 2 | 4 | -1 | -8 | -2 | -4 |
| 2x+1 | 8 | 1 | 4 | 2 | -8 | -1 | -4 | -2 |
| y(yϵ\(ℤ\)) | 5/2(loại ) | 6(thỏa mãn) | 3(loại) | 4(loại) | 3/2( loại) | -2(thỏa mãn) | 1( loại) | 0(loại ) |
| x(xϵ\(ℤ\)) | 7/2(loại) | 0(thỏa mãn) | 3/2( loại) | 1/2( loại) | -9/2( loại) | -1(thỏa mãn) | -5/2( loại) | -3/2( loại) |
Vậy các cặp nghiệm x,y thỏa mãn là (0;6) và (-1;-2)
PT
2
HN
28 tháng 10 2019
Ta có : x - y + 2xy = 7
=> ( x + 2xy ) - y = 7
=> x ( 1 + 2y ) - 1/2 ( 2y + 1 ) + 1/2 = 7
=> ( 2y + 1 ) ( x - 1/2 ) = 7 - 1/2
=> ( 2y + 1 ) ( x - 1/2 ) = 13/2
=> ( 2y + 1 ) 2( x - 1/2 ) = 13/2 . 2
=> ( 2y + 1 ) ( 2x - 1 ) = 13 (1)
Với mọi x,y ta có : 2y + 1; 2x - 1 thuộc Z và 2y + 1; 2x - 1 đều là số lẻ
Nên từ (1) ta có
( 2y + 1 ) ( 2x - 1) = 1 . 13 = 13 . 1 = -1 . ( - 13 ) = -13 . (-1)
Từ đó tìm ra x,y thỏa mãn
28 tháng 10 2019
\(x-y+2xy=7\)
\(2xy+x-y=7\)
\(x\left(2y+1\right)-y=7\)
\(2x\left(2y+1\right)-2y=14\)
\(2x\left(2y+1\right)-\left(2y+1\right)=13\)
\(\left(2y+1\right)\left(2x-1\right)=13\)
Xét bảng:
| \(2y+1\) | 13 | 1 | -13 | -1 |
| \(2x-1\) | 1 | 13 | -1 | -13 |
| \(x\) | 1 | 7 | 0 | -6 |
| \(y\) | 6 | 0 | -7 | -1 |
Vậy................