

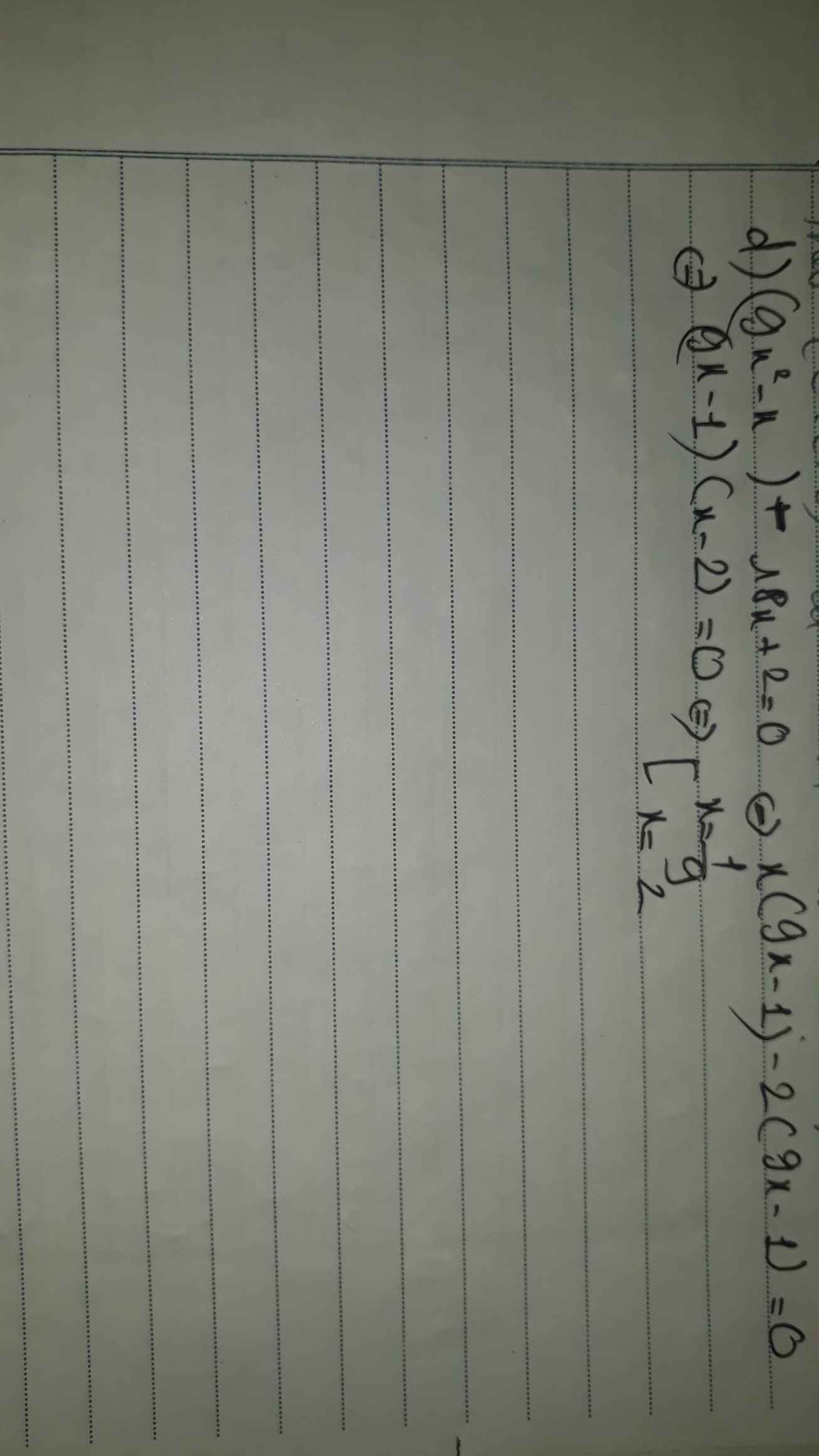
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


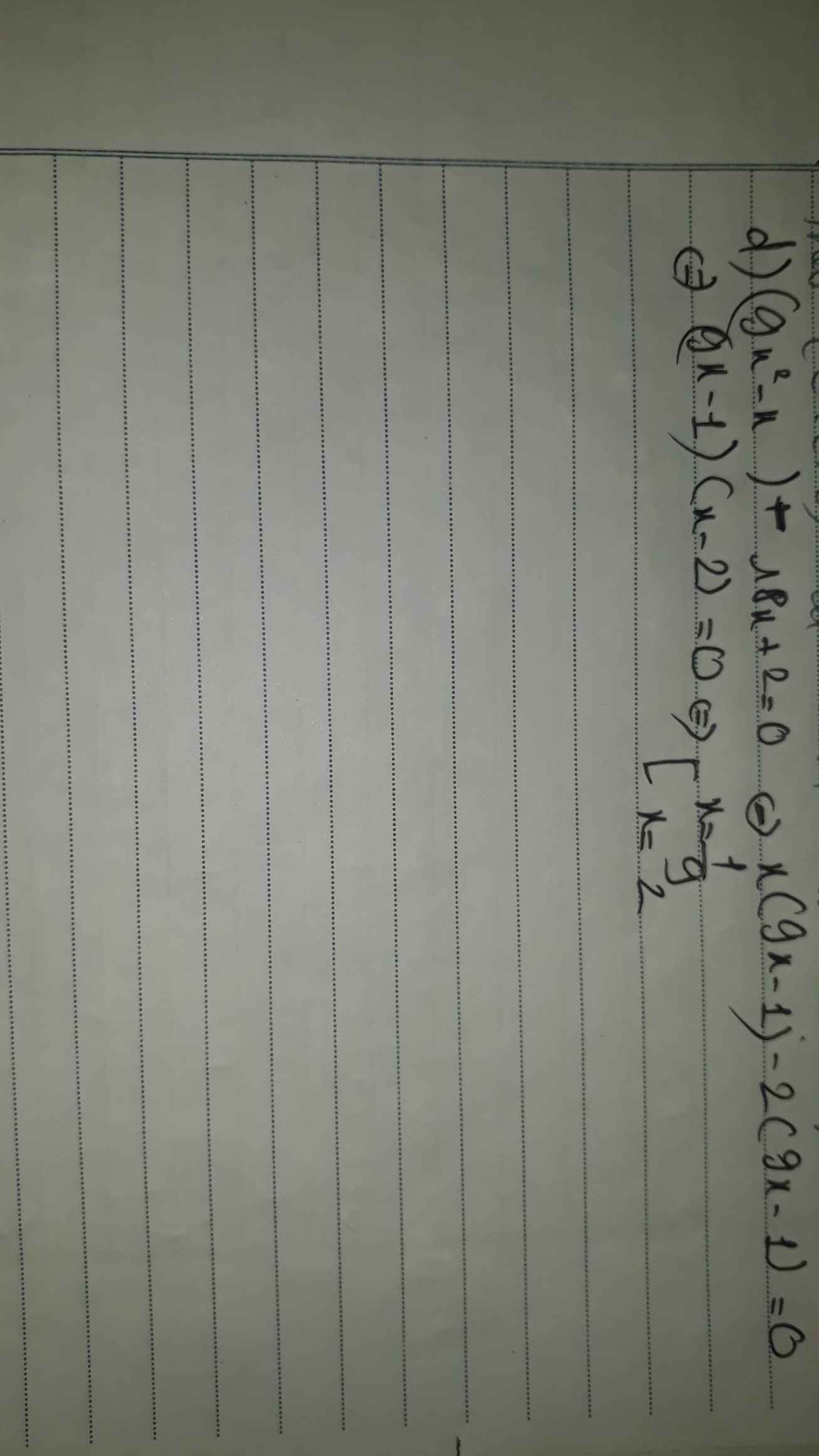

nhiều quá bạn ạ
hay bạn tìm hiểu cách thức chung làm dạng bài tìm GTNN chứ như thế này thì làm lâu lắm
mik chỉ tìm hiểu đc đến câu I còn lại mik k hiểu lắm, bn có lm đc k, giúp mik vs

1) \(\left(x-3\right)\left(x-5\right)+44\)
\(=x^2-3x-5x+15+44\)
\(=x^2-8x+59\)
\(=x^2-2.x.4+4^2+43\)
\(=\left(x-4\right)^2+43\ge43>0\)
\(\rightarrowĐPCM.\)
2) \(x^2+y^2-8x+4y+31\)
\(=\left(x^2-8x\right)+\left(y^2+4y\right)+31\)
\(=\left(x^2-2.x.4+4^2\right)-16+\left(y^2+2.y.2+2^2\right)-4+31\)
\(=\left(x-4\right)^2+\left(y+2\right)^2+11\ge11>0\)
\(\rightarrowĐPCM.\)
3)\(16x^2+6x+25\)
\(=16\left(x^2+\dfrac{3}{8}x+\dfrac{25}{16}\right)\)
\(=16\left(x^2+2.x.\dfrac{3}{16}+\dfrac{9}{256}-\dfrac{9}{256}+\dfrac{25}{16}\right)\)
\(=16\left[\left(x+\dfrac{3}{16}\right)^2+\dfrac{391}{256}\right]\)
\(=16\left(x+\dfrac{3}{16}\right)^2+\dfrac{391}{16}>0\)
-> ĐPCM.
4) Tương tự câu 3)
5) \(x^2+\dfrac{2}{3}x+\dfrac{1}{2}\)
\(=x^2+2.x.\dfrac{1}{3}+\dfrac{1}{9}-\dfrac{1}{9}+\dfrac{1}{2}\)
\(=\left(x+\dfrac{1}{3}\right)^2+\dfrac{7}{18}>0\)
-> ĐPCM.
6) Tương tự câu 5)
7) 8) 9) Tương tự câu 3).

a) \(3\left(2x-1\right)\left(3x-1\right)-\left(2x-3\right)\left(9x-1\right)-3=-3\)
\(\Leftrightarrow18x^2-15x+3-18x^2+29x-3-3=-3\)
\(\Leftrightarrow14x=0\)
\(\Leftrightarrow x=0\)
Vậy pt có nghiệm duy nhất x = 0.
b) \(\left(3x-1\right)\left(2x+7\right)-\left(x+1\right)\left(6x-5\right)=\left(x+2\right)-\left(x-5\right)\)
\(\Leftrightarrow6x^2+19x-7-6x^2-x+5=7\)
\(\Leftrightarrow18x-2=7\)
\(\Leftrightarrow18x=9\)
\(\Leftrightarrow x=\frac{1}{2}\)
Vậy pt có nghiệm duy nhất \(x=\frac{1}{2}\)
c) \(\left(6x-2\right)^2+\left(5x-2\right)^2-4\left(3x-1\right)\left(5x-2\right)=0\)
\(\Leftrightarrow36x^2-24x+4+25x^2-20x+4-60x^2+33x-8=0\)
\(\Leftrightarrow x^2-11x=0\)
\(\Leftrightarrow x\left(x-11\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=11\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{0;11\right\}\)
d) \(\left(x+3\right)^2-\left(x-4\right)\left(x+8\right)=1\)
\(\Leftrightarrow x^2-6x+9-x^2-4x+32=1\)
\(\Leftrightarrow41-10x=1\)
\(\Leftrightarrow-10x=40\)
\(\Leftrightarrow x=-4\)
Vậy pt có nghiệm duy nhất x = -4.
e) \(3\left(x+2\right)^2+\left(2x-1\right)^2-7\left(x+3\right)\left(x-3\right)=36\)
\(\Leftrightarrow3\left(x^2+4x+4\right)+4x^2-4x+1-7x^2+36=36\)
\(\Leftrightarrow3x^2+12x+12+4x^2-4x+1-7x^2=0\)
\(\Leftrightarrow8x=-13\)
\(\Leftrightarrow x=-\frac{13}{8}\)
Vậy pt có nghiệm duy nhất \(x=-\frac{13}{8}\)

a) \(\dfrac{x+1}{2}+\dfrac{3x-2}{3}=\dfrac{x-7}{12}\)
\(\Leftrightarrow\dfrac{6\left(x+1\right)+4\left(3x-2\right)}{12}=\dfrac{x-7}{12}\)
\(\Leftrightarrow6\left(x+1\right)+4\left(3x-2\right)=x-7\)
\(\Leftrightarrow6x+6+12x-8=x-7\)
\(\Leftrightarrow6x+12x-x=-7-6+8\)
\(\Leftrightarrow17x=-5\)
\(\Leftrightarrow x=\dfrac{-5}{17}\)
Vậy .........................
b) \(\dfrac{2x}{x-3}-\dfrac{5}{x+3}=\dfrac{x^2+21}{x^2-9}\left(ĐKXĐ:x\ne\pm3\right)\)
\(\Leftrightarrow\dfrac{2x\left(x+3\right)-5\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{x^2+21}{\left(x-3\right)\left(x+3\right)}\)
\(\Rightarrow2x\left(x+3\right)-5\left(x-3\right)=x^2+21\)
\(\Leftrightarrow2x^2+6x-5x+15=x^2+21\)
\(\Leftrightarrow2x^2-x^2+x+15-21=0\)
\(\Leftrightarrow x^2+x-6=0\)
\(\Leftrightarrow x^2-2x+3x-6=0\)
\(\Leftrightarrow x\left(x-2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(n\right)\\x=-3\left(l\right)\end{matrix}\right.\)
Vậy \(S=\left\{2\right\}\)
d) \(\left(x-4\right)\left(7x-3\right)-x^2+16=0\)
\(\Leftrightarrow\left(x-4\right)\left(7x-3\right)-\left(x^2-16\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(7x-3\right)-\left(x-4\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(7x-3-x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(6x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\6x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{7}{6}\end{matrix}\right.\)
Vậy .........................
P/s: các câu còn lại tương tự, bn tự giải nha

Bài 1.
a) x( 8x - 2 ) - 8x2 + 12 = 0
<=> 8x2 - 2x - 8x2 + 12 = 0
<=> 12 - 2x = 0
<=> 2x = 12
<=> x = 6
b) x( 4x - 5 ) - ( 2x + 1 )2 = 0
<=> 4x2 - 5x - ( 4x2 + 4x + 1 ) = 0
<=> 4x2 - 5x - 4x2 - 4x - 1 = 0
<=> -9x - 1 = 0
<=> -9x = 1
<=> x = -1/9
c) ( 5 - 2x )( 2x + 7 ) = ( 2x - 5 )( 2x + 5 )
<=> -4x2 - 4x + 35 = 4x2 - 25
<=> -4x2 - 4x + 35 - 4x2 + 25 = 0
<=> -8x2 - 4x + 60 = 0
<=> -8x2 + 20x - 24x + 60 = 0
<=> -4x( 2x - 5 ) - 12( 2x - 5 ) = 0
<=> ( 2x - 5 )( -4x - 12 ) = 0
<=> \(\orbr{\begin{cases}2x-5=0\\-4x-12=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{5}{2}\\x=-3\end{cases}}\)
d) 64x2 - 49 = 0
<=> ( 8x )2 - 72 = 0
<=> ( 8x - 7 )( 8x + 7 ) = 0
<=> \(\orbr{\begin{cases}8x-7=0\\8x+7=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{7}{8}\\x=-\frac{7}{8}\end{cases}}\)
e) ( x2 + 6x + 9 )( x2 + 8x + 7 ) = 0
<=> ( x + 3 )2( x2 + x + 7x + 7 ) = 0
<=> ( x + 3 )2 [ x( x + 1 ) + 7( x + 1 ) ] = 0
<=> ( x + 3 )2( x + 1 )( x + 7 ) = 0
<=> x = -3 hoặc x = -1 hoặc x = -7
g) ( x2 + 1 )( x2 - 8x + 7 ) = 0
Vì x2 + 1 ≥ 1 > 0 với mọi x
=> x2 - 8x + 7 = 0
=> x2 - x - 7x + 7 = 0
=> x( x - 1 ) - 7( x - 1 ) = 0
=> ( x - 1 )( x - 7 ) = 0
=> \(\orbr{\begin{cases}x-1=0\\x-7=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=1\\x=7\end{cases}}\)
Bài 2.
a) ( x - 1 )2 - ( x - 2 )( x + 2 )
= x2 - 2x + 1 - ( x2 - 4 )
= x2 - 2x + 1 - x2 + 4
= -2x + 5
b) ( 3x + 5 )2 + ( 26x + 10 )( 2 - 3x ) + ( 2 - 3x )2
= 9x2 + 30x + 25 - 78x2 + 22x + 20 + 9x2 - 12x + 4
= ( 9x2 - 78x2 + 9x2 ) + ( 30x + 22x - 12x ) + ( 25 + 20 + 4 )
= -60x2 + 40x2 + 49
d) ( x + y )2 - ( x + y - 2 )2
= [ x + y - ( x + y - 2 ) ][ x + y + ( x + y - 2 ) ]
= ( x + y - x - y + 2 )( x + y + x + y - 2 )
= 2( 2x + 2y - 2 )
= 4x + 4y - 4
Bài 3.
A = 3x2 + 18x + 33
= 3( x2 + 6x + 9 ) + 6
= 3( x + 3 )2 + 6 ≥ 6 ∀ x
Đẳng thức xảy ra <=> x + 3 = 0 => x = -3
=> MinA = 6 <=> x = -3
B = x2 - 6x + 10 + y2
= ( x2 - 6x + 9 ) + y2 + 1
= ( x - 3 )2 + y2 + 1 ≥ 1 ∀ x,y
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x-3=0\\y^2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=3\\y=0\end{cases}}\)
=> MinB = 1 <=> x = 3 ; y = 0
C = ( 2x - 1 )2 + ( x + 2 )2
= 4x2 - 4x + 1 + x2 + 4x + 4
= 5x2 + 5 ≥ 5 ∀ x
Đẳng thức xảy ra <=> 5x2 = 0 => x = 0
=> MinC = 5 <=> x = 0
D = -2/7x2 - 8x + 7 ( sửa thành tìm Max )
Để D đạt GTLN => 7x2 - 8x + 7 đạt GTNN
7x2 - 8x + 7
= 7( x2 - 8/7x + 16/49 ) + 33/7
= 7( x - 4/7 )2 + 33/7 ≥ 33/7 ∀ x
Đẳng thức xảy ra <=> x - 4/7 = 0 => x = 4/7
=> MaxC = \(\frac{-2}{\frac{33}{7}}=-\frac{14}{33}\)<=> x = 4/7

Bài 2: a) \(3x^3-3x=0\Leftrightarrow3x\left(x^2-1\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm1\end{cases}}\)
b) \(x^2-x+\frac{1}{4}=0\Leftrightarrow x^2-2.\frac{1}{2}+\left(\frac{1}{2}\right)^2=0\Leftrightarrow\left(x-\frac{1}{2}\right)^2=0\)
\(\Leftrightarrow x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}\)

\(x^2-2x=24\)
<=> \(x^2-2x-24=0\)
<=> \( \left(x+4\right)\left(x-6\right)=0\)
<=> \(\orbr{\begin{cases}x=-4\\x=6\end{cases}}\)
Vậy....
\(a,\left(x+2\right)^2-x^2+4=0\)
\(\Leftrightarrow\left(x+2\right)^2+4-x^2=0\)
\(\Leftrightarrow\left(2+x\right)^2+\left(2-x\right)\left(2+x\right)=0\)
\(\Leftrightarrow\left(2+x\right)\left(2+x+2-x\right)=0\)
\(\Leftrightarrow4\left(2+x\right)=0\)
\(\Leftrightarrow2+x=0\)
\(\Leftrightarrow x=-2\)
\(c,\left(2x-1\right)^2+\left(x+3\right)^2-5\left(x+7\right)\left(x-7\right)=0\)
\(\Leftrightarrow4x^2-4x+1+x^2+6x+9-5\left(x^2-49\right)=0\)
\(\Leftrightarrow5x^2+2x+10-5x^2+245=0\)
\(\Leftrightarrow2x+255=0\)
\(\Leftrightarrow x=-127,5\)

Bài 1a/
\(\frac{1}{1+x+xy}=\frac{xyz}{xyz+x+xy}=\frac{yz}{1+y+yz}\)
\(\frac{1}{1+z+xz}=\frac{y}{y+yz+xyz}=\frac{y}{1+y+yz}\)
Vậy \(M=\frac{1}{1+y+yz}+\frac{y}{1+y+yz}+\frac{yz}{1+y+yz}=1\)
Chiều về làm tiếp
Bài 1b:Lời giải này chủ yếu nhờ dự đoán trước Min là 2011/2012 đạt được khi x=2012
Ta có \(P=\frac{2012x^2-2.2012x+2012^2}{2012x^2}=\frac{\left(x-2012\right)^2+2011x^2}{2012x^2}\ge\frac{2011x^2}{2012x^2}=\frac{2011}{2012}\)
Bài 2: Dùng phân tích thành bình phương
\(10x^2+y^2+4z^2+6x-4y-4xz+5=\left(9x^2+6x+1\right)+\left(y^2-4y+4\right)+\left(x^2-4xz+4z^2\right)\)
\(=\left(3x+1\right)^2+\left(y-2\right)^2+\left(x-2z\right)^2=0\)
\(\Rightarrow\hept{\begin{cases}3x+1=0\\y-2=0\\x-2z=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{-1}{3}\\y=2\\z=-\frac{1}{6}\end{cases}}}\)
Bài 3:
a/\(pt\Leftrightarrow\left(x+6\right)\left(x-5\right)\left(x^2-x+1\right)=0\Leftrightarrow x=-6,x=5\)
b/ta phân tích vế trái thành:\(\left(3x-3\right)^2+\left(y-3\right)^2+2\left(z+1\right)^2=0\Rightarrow\hept{\begin{cases}x=1\\y=3\\z=-1\end{cases}}\)

a, 2(x+5)=x2+5x
=> 2x+10=x2+5x
=> 0=x2+5x-2x-10
=> x2+3x-10=0
=> x2+5x-2x-10=0
=> x(x+5)-2(x+5)=0
=> (x-2)(x+5)=0
=> x-2 =0 hoặc x+5 =0
=> x=2 hoặc x=-5
b, 4x2-25=(2x-5)(2x+7)
=> (2x)2-52=(2x-5)(2x+7)
=> (2x-5)(2x+5) - (2x-5)(2x+7)=0
=> (2x-5)(2x+5-2x-7)=0
=> (2x-5)(-2)=0
=> 2x-5=0
=> 2x=5
=> x =2,5
c, x3+x=0
=>x(x2+1)=0
=> x=0 hoặc x2+1=0
Mà x2+1 >= 1 nên x=0
d, Hình như là thiếu đề
a,=2x+10=x2+5x
=-x2-2x-5x+10=0
=-x2-7x+10=0
Delta=(-7)2-4.-1.10=89
x1=7+căn89/2 x2=7-căn 89/2
CÁC CÂU KHÁC TỰ GIẢI NHA bạn