JG
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DM
2
PT
0
TN
1
HP
21 tháng 3 2016
Ta có:x2-2y2=1
<=>x2-1=2y2
<=>(x-1)(x+1)=2y2=y.2y
TH1:(x-1)(x+1)=2y2
=>x-1=2 và x+1=y2
=>x=3 và x+1=y2=>y2=3+1=4=>y=2
TH2:(x-1)(x+1)=y.2y
=>x-1=y và x+1=2y
=>x=y+1 (*)
và x+1=2y
ta có x+1=2y, kết hợp với (*)
=>(y+1)+1=2y=>y+2=2y=>2y-y=2=>y=2
Khi đó x=2+1=3
Vậy (x;y)=(3;2)
LM
1
5 tháng 3 2015
Ta có: x2-2y2=1
x2-1=2y2(x-1)(x+1)=2y2
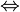x2-1=2y2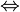(x-1)(x+1)=2y2vì 2y2\( {\vdots}\)2 nên (x-1)(x+1)\( {\vdots}\)2
vì x-1+x+1=2x 
x-1 và x+1 có cùng tính chẵn lẻ
(x-1)(x+1) là hai số chẵn liên tiếp
(x-1)(x+1)\( {\vdots}\)4 2y2\( {\vdots}\)4 y2\( {\vdots}\)2 y\( {\vdots}\)2 y = 2
Và từ y=2 ta thay vào x2-2y2=1 x2-2.22=1 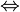x2 = 9 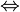x = 3
Vật số nguyên tố (x, y) là cặp số (3, 2)
AT
0
LL
14 tháng 5 2018
Cho ba đa thức
P(x) = y3 - 2y2 + 3y + 1
Q(x) = y3 + y + 1
H(x) = 2y2 - 1
a) Hãy tính P(x) - Q(x) + H(x)
P(x) - Q(x) + H(x)
= (y3 - 2y2 + 3y + 1) - (y3 + y + 1) + (2y2 - 1)
= y3 - 2y2 + 3y + 1 - y3 - y - 1 + 2y2 - 1
= 2y - 1
b) Tìm y sao cho P(x) - Q(x) + H(x) =0
P(x) - Q(x) + H(x) = 0 <=> 2y - 1 = 0 <=> 2y = 1 <=> y = 1/2
HB
1
+ Nếu y = 3 => ko tồn tại x thuộc P
+ Nếu y khác 3 => y ko chia hết cho 3 => y^2 chia 3 dư 1 => 2y^2 chia 3 dư 2 => x^2 chia hết cho 3
=> x chia hết cho 3 ( vì 3 là số nguyên tố )
=> x = 3
=> y = 2
Vậy ........
Tk mk nha
Biến đổi biểu thức tương đương: \(x^2-2y^2=1\Leftrightarrow\frac{x^2-1}{2}=y^2\)
Vì x,y là số nguyên dương nên
- x > y và x phải là số lẽ suy ra đặt x = 2k + 1 ( k nguyên dương )
Biểu thức tương đương \(2.k.\left(k+1\right)=y^2\left(1\right)\)
Y là 1 số nguyên tố nên y^2 sẽ là 1 số nguyên dương mà nó có duy nhất 3 ước là : \(\left\{1;y;y^2\right\}\)
Từ ( 1 ) ta dễ dàng thấy y^2 chia hết cho 2 và y^2 không thể chia hết cho 2 nên suy ra y = 2
Suy ra k = 1 và x = 3
Vậy ta chỉ tìm được 1 cặp số nguyên tố thoả mãn bài ra là x = 3 và y = 2