K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
31 tháng 10 2018
a)(2x+1).(y-3)=10
có:10=1.10=2.5=10.1=5.2
xét:2x+1=1 ; y-3=10
2x=1-1=0 y=10+3=13(nhận)
x=0:2=0(nhận)
......(xét tiếp các trường hợp còn lại)
Vậy............
b)(3x-2).(2y-3)=1
\(\Leftrightarrow\) 3x-2=1 hoặc 2y-3=1
3x=1+2=3 2y=1+3=4
x=3:3=1 y=4:2=2
Vậy x=1 và y=2
c làm tương tự phần a
NB
1
17 tháng 12 2022
Ta thấy (x+1)(2y-5)=143=11.13=13.11=143.1=1.143
Suy ra ta có 4 trường hợp sau:
-Nếu x+1=11suy ra x=10 ; 2y-5=13 suy ra y=9
-Nếu x+1=13 suy ra x=12 ; 2y-5=11 suy ra y=8
-Nếu x+1=143 suy ra x=142 ; 2y-5=1 suy ra y=3
-Nếu x+1=1 suy ra x=0 ; 2y-5=143 suy ra y=74
Vậy x=10 thì y=9
x=12 thì y=8
x=142 thì y=3
x=0 thì y=74
AH
Akai Haruma
Giáo viên
30 tháng 4 2023
Lời giải:
$\frac{1}{x}+\frac{1}{y}=\frac{1}{8}$
$\Rightarrow \frac{x+y}{xy}=\frac{1}{8}$
$\Rightarrow 8(x+y)=xy$
$\Rightarrow xy-8x-8y=0$
$\Rightarrow x(y-8)-8(y-8)=64$
$\Rightarrow (x-8)(y-8)=64$
Do $x,y$ tự nhiên nên $x-8,y-8\in\mathbb{Z}$
$\Rightarrow x-8$ là ước của $64$. Mà $x-8>-8$ với mọi $x\in\mathbb{N}^*$ nên:
$x-8\in\left\{1; 2; 4; 8; 16; 32; 64; -1; -2; -4\right\}$
Đến đây bạn chỉ cần chịu khó xét các TH là được.
18 tháng 11 2016
1. Tìm x,y biết: ( x,y thuộc N)
a) (2x+1) (y-3) =10
Ta có: 10 = 2.5
=> 2x+1=5
=> y-3=2
Để 2x+1=5 => 2x=4=> x= 2
Để y-3=2 => y= 4
Vậy x=2 ; y=4
18 tháng 11 2016
1. Tìm x,y biết: ( x,y thuộc N)
a) (2x+1) (y-3) =10
Ta có: 10 = 2.5
=> 2x+1=5
=> y-3=2
Để 2x+1=5 => 2x=4=> x= 2
Để y-3=2 => y= 4
Vậy x=2 ; y=4
@phynit
13 tháng 1 2022
Bài 2:
a: =>x=0 hoặc x+3=0
=>x=0 hoặc x=-3
b: =>x-2=0 hoặc 5-x=0
=>x=2 hoặc x=5
c: =>x-1=0
hay x=1
BJ
Tìm x,y thuộc N biết:
a/ ( 3.x-2).(2y-3)=1
b/ (x-5).(x+1)=7
c/ (x+1)>(2y-1)=10
giải giúp mik bài này nhé
1
19 tháng 12 2015
a)(3x-2)(2y-3)=1
Ta xét bảng sau:
| 3x-2 | 1 |
| 3x | 3 |
| x | 1 |
| 2y-3 | 1 |
| 2y | 4 |
| y | 2 |
b)(x-5)(x+1)=7
Ta xét bảng sau:
| x-5 | 1 | 7 |
| x | 6 | 12 |
| x+1 | 7 | 1 |
| x | 6 | 0 |
=>x=6
c)mk chả hiểu cậu ghi j hết
TC
1
AH
Akai Haruma
Giáo viên
24 tháng 9 2023
Lời giải:
a. $2y(3x-1)+9x-3=7$
$2y(3x-1)+3(3x-1)=7$
$(3x-1)(2y+3)=7$
Vì $3x-1, 2y+3$ đều là số nguyên với mọi $x,y\in N$, và $2y+3>0$ nên ta có bảng sau: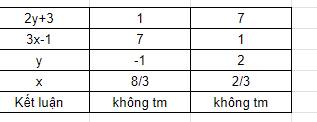
b.
$3xy-2x+3y-9=0$
$x(3y-2)+3y-9=0$
$x(3y-2)+(3y-2)-7=0$
$(3y-2)(x+1)=7$
Đến đây bạn cũng lập bảng tương tự như phần a.
Lời giải:
Vì $x,y\in\mathbb{N}$ nên $x-1, 2y-1\in\mathbb{Z}$
Mà $(x-1)(2y-1)=10$ và $2y-1$ lẻ nên ta có các TH sau:
TH1:
$x-1=10; 2y-1=1\Rightarrow x=11; y=1$
TH2:
$x-1=-10; 2y-1=-1\Rightarrow x=-9; y=0$
TH3:
$x-1=2, 2y-1=5\Rightarrow x=3; y=3$
TH4:
$x-1=-2; 2y-1=-5\Rightarrow x=-1; y=-2$