
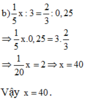
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

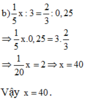

Bài 1:
a) \(\frac{x}{-15}=\frac{-60}{x}\Rightarrow x^2=\left(-60\right).\left(-15\right)=900\Rightarrow x=\orbr{\begin{cases}30\\-30\end{cases}}\)
Bài 2: Đặt \(\frac{x}{4}=\frac{y}{7}=k\Rightarrow x=4k;y=7k\)
\(\Rightarrow xy=4k.7k=28k^2=112\)
\(\Rightarrow k^2=4\Rightarrow k=\pm2\)
\(\Rightarrow\orbr{\begin{cases}x=4.2=8\\x=-4.2=-8\end{cases}}\)
Và \(\orbr{\begin{cases}y=7.2=14\\y=-7.2=-14\end{cases}}\)
Bài 3: \(1\frac{1}{3}:0,8=\frac{2}{3}:\left(0,1x\right)\)
\(\Rightarrow\frac{4}{3}:\frac{4}{5}=\frac{2}{3}:\frac{1}{10}x\Rightarrow\frac{5}{3}=\frac{2}{3}:\frac{1}{10}x\)
\(\Rightarrow\frac{1}{10}x=\frac{2}{5}\Rightarrow x=4\)
Mk trả lời nốt bài 4 hộ bn MMS_Hồ Khánh Châu nha:
Bài 4:
Gọi x là giá trị chung của 2 phân số trên.
Ta có: \(\frac{a}{b}=\frac{c}{d}=x\)
\(\Rightarrow a=x.b
\)
\(c=x.d\)
Ta lại có:
\(\frac{a+c}{b+d}=\frac{x.b+x.d}{b+d}=\frac{x.\left(b+d\right)}{b+d}=x\)
Và \(\frac{a}{b}=x\)
\(\Rightarrow\frac{a}{b}=\frac{a+c}{b+d}\)
Vậy \(\frac{a}{b}=\frac{a+c}{b+d}\)
Hk tốt nha

a) \(\frac{3x-2}{1\frac{2}{5}}=\frac{2\frac{3}{7}}{2\frac{3}{5}}\Rightarrow3x-2=1.\frac{2}{5}.\frac{2\frac{3}{7}}{2\frac{3}{5}}=\frac{7}{5}.\frac{17}{7}.\frac{5}{13}\)
\(3x-2=\frac{17}{13}\Rightarrow3x=2+\frac{17}{13}=\frac{43}{13}\Rightarrow x=\frac{43}{39}.\)
b) \(\frac{x}{0,16}=\frac{9}{x}\Rightarrow x^2=9.0,16=1,44\Rightarrow x=\pm1,2\)


P/s : Vì bạn lớp 7 nên mình giải chi tiết nha!
Có \(\frac{x-1}{x+2}=\frac{x-2}{x+3}\Leftrightarrow\left(x-1\right)\left(x+3\right)=\left(x+2\right)\left(x-2\right)\)
\(\Leftrightarrow x\left(x+3\right)-1\left(x+3\right)=x\left(x-2\right)+2\left(x-2\right)\)
\(\Leftrightarrow x^2+3x-x-3=x^2-2x+2x-4\)
\(\Leftrightarrow x^2+\left(3x-x\right)-3=x^2+\left(2x-2x\right)-4\)
\(\Leftrightarrow x^2+2x-3=x^2-4\Leftrightarrow x^2-x^2+2x=3-4=-1\)
\(=\left(x^2-x^2\right)+2x=-1\Leftrightarrow2x=1\Leftrightarrow x=1\div2=\frac{1}{2}\)

a) \(2,5:0,4x=0,5:0,2\)
\(\Rightarrow\frac{5}{2}:4x=\frac{1}{2}:\frac{1}{5}=\frac{5}{2}\)
\(\Rightarrow4x=\frac{5}{2}:\frac{5}{2}=1\)
\(\Rightarrow x=\frac{1}{4}\)
b) \(\frac{1}{5}x:3=\frac{2}{3}:0,25\)
\(\Rightarrow\frac{1}{5}x:3=\frac{8}{3}\)
\(\Rightarrow\frac{1}{5}x=\frac{8}{3}.3=8\Rightarrow x=40\)
a)2,5:4x=0,5:0,2
2,5:4x=2.5
4x=2,5:2,5
4x=1
x=1:4
x=0,25

\(\frac{x-1}{x-2}=\frac{x+3}{x+4}\)
\(\Rightarrow\left(x-1\right)\left(x+4\right)=\left(x-2\right)\left(x+3\right)\)
\(\Leftrightarrow x^2+4x-x-4=x^2+3x-2x-6\)
\(\Leftrightarrow x^2+4x-x-4-x^2-3x+2x+6=0\)
\(\Leftrightarrow2x+2=0\)
\(\Leftrightarrow2x=-2\)
\(\Leftrightarrow x=-1\)VẬY X=-1 LÀ NGHIỆM CỦA PHƯƠNG TRÌNH \(\frac{x-1}{x-2}=\frac{x+3}{x+4}\)

1) a) Ta có: \(\frac{x}{-15}=\frac{-60}{x}\) \(\Rightarrow x^2=\left(-15\right).\left(-60\right)=900\)
\(\Rightarrow x=30\)
b) \(\frac{-2}{x}=\frac{-x}{\frac{8}{25}}\) \(\Rightarrow x.\left(-x\right)=\left(-2\right).\frac{8}{25}\)
\(\Rightarrow x.\left(-x\right)=\frac{-16}{25}\)
\(\Rightarrow x.\left(-x\right)=\left(\frac{-4}{5}\right).\frac{4}{5}\)
Vậy \(x=\frac{4}{5}\)
2) a) \(3,8: \left(2x\right)=\frac{1}{4}:2\frac{2}{3}\)
\(\Rightarrow3,8: \left(2x\right)=\frac{3}{32}\)
\(\Rightarrow2x=\frac{3}{32}:3,8=\frac{15}{608}\)
\(x=\frac{15}{608}:2=\frac{15}{1216}\)
Vậy \(x=\frac{15}{1216}\)
b) \(\left(0,25x\right):3=\frac{5}{6}:0,125\)
\(\Rightarrow\left(0,25x\right):3=\frac{20}{3}\)
\(\Rightarrow0,25x=\frac{20}{3}.3=20\)
\(\Rightarrow x=20:0,25=80\)
Vậy x = 80
c) \(0,01:2,5=\left(0,75x\right):0,75\)
\(\Rightarrow\frac{1}{250}=\left(0,75x\right):0,75\)
\(\Leftrightarrow0,75x=\frac{1}{250}.0,75=\frac{3}{1000}\)
\(\Rightarrow x=\frac{3}{1000}:0,75=\frac{1}{250}\)
Vậy \(x=\frac{1}{250}\)
d) \(1\frac{1}{3}:0,8=\frac{2}{3}:\left(0,1x\right)\)
\(\Rightarrow\frac{5}{3}=\frac{2}{3}:\left(0,1x\right)\)
\(\Rightarrow0,1x=\frac{5}{3}.\frac{2}{3}=\frac{10}{9}\)
\(\Rightarrow x=\frac{10}{9}:0,1=\frac{100}{9}\)
Vậy \(x=\frac{100}{9}\)
a) \(\frac{x}{-15}=\frac{-60}{x}\Leftrightarrow x.x=-15.\left(-60\right)\Leftrightarrow x^2=900\Leftrightarrow x^2=\orbr{\begin{cases}30^2\\\left(-30\right)^2\end{cases}}\Leftrightarrow x=\orbr{\begin{cases}30\\-30\end{cases}}\)