Tìm x ∈ Q, biết rằng: (x - (1/2))2 = 0

K

Khách

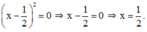
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

17 tháng 4 2019

Tìm x ∈ Q, biết rằng: (x - (1/2))2 = 0

#Hỏi cộng đồng OLM #Toán lớp 7

1

CM

Cao Minh Tâm

17 tháng 4 2019

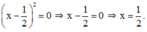
Giải sách bài tập Toán 7 | Giải sbt Toán 7

Các câu hỏi dưới đây có thể giống với câu hỏi trên

NT

Nguyễn Thu Hà

24 tháng 7 2018 - olm

Tìm x biết rằng:

\(\left([x]+2\right)\)x\(\left(3[x]-1\right)\)=0

#Hỏi cộng đồng OLM #Toán lớp 7

2

DL

Dương Lam Hàng

24 tháng 7 2018

\(\left(x+2\right)\times\left(3x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\3x-1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=-2\\x=\frac{1}{3}\end{cases}}}\)

Vậy x = -2 hoặc x = 1/3

NT

Nguyễn Thu Hà

24 tháng 7 2018

Cảm ơn bạn MMS_Hồ Khánh Châu nheee :))

Nhưng mà bạn đọc kĩ lại đề bài đii

Đây là giá trị nguyên của x mà

NT

Nguyễn Thị Phương Thảo

11 tháng 2 2018

tìm giá trị các biểu thức sau: 1/ 3x\(^4\)+5x\(^2\)y\(^2\)+2y\(^4\)+2y\(^2\) biết rằng x\(^2\)+y\(^2\)=1 2/ 7x-7y+4ax-4ay-5 biết x-y=0 3/ x\(^3\)+xy\(^2\)-x\(^2\)y-y\(^3\)+3 biết x-y=0 4/ x\(^2\)+2xy+y\(^2\)-4x-4y+1 biết rằng x+y=3 giup voi mk dang...

#Hỏi cộng đồng OLM #Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

19 tháng 6 2022

1: \(=3x^4+3x^2y^2+2x^2y^2+2y^4+2y^2\)

\(=\left(x^2+y^2\right)\left(3x^2+2y^2\right)+2y^2\)

\(=3x^2+2y^2+2y^2=3x^2+4y^2\)

2: \(=7\left(x-y\right)+4a\left(x-y\right)-5\)

=-5

3: \(=\left(x-y\right)\left(x^2+xy+y^2\right)-xy\left(x-y\right)+3=3\)

4: \(=\left(x+y\right)^2-4\left(x+y\right)+1=9-12+1=-2\)

GV

Gốc Việt

27 tháng 6 2017 - olm

tìm x thuộc Q, biết rằng :

a) \(\left(x-\frac{1}{2}\right)^2=0\)

b)\(\left(x-2\right)^2=1\)

c) \(\left(2x-1\right)^3=-8\)

d) \(\left(x+\frac{1}{2}\right)^2=\frac{1}{16}\)

#Hỏi cộng đồng OLM #Toán lớp 7

2

TT

Thanh Tùng DZ

27 tháng 6 2017

a) \(\left(x-\frac{1}{2}\right)^2=0\)

\(x-\frac{1}{2}=0\)

\(x=0+\frac{1}{2}\)

\(x=\frac{1}{2}\)

b) \(\left(x-2\right)^2=1\)

\(\left(x-2\right)^2=1^2\)

\(x-2=1\)

\(x=1+2\)

\(x=3\)

c) \(\left(2x-1\right)^3=\left(-8\right)\)

\(\left(2x-1\right)^3=\left(-2\right)^3\)

\(2x-1=\left(-2\right)\)

\(2x=\left(-2\right)+1\)

\(2x=-1\)

\(x=-\frac{1}{2}\)

d) \(\left(x+\frac{1}{2}\right)^2=\frac{1}{16}\)

\(\left(x+\frac{1}{2}\right)^2=\left(\frac{1}{4}\right)^2\)

\(x+\frac{1}{2}=\frac{1}{4}\)

\(x=\frac{1}{4}-\frac{1}{2}\)

\(x=-\frac{1}{4}\)

LT

lê thị thu huyền

27 tháng 6 2017

a) \(\left(x-\frac{1}{2}\right)^2=0\)

\(\Leftrightarrow x-\frac{1}{2}=0\)

\(\Leftrightarrow x=\frac{1}{2}\)

b) \(\left(x-2\right)^2=1\)

\(\Leftrightarrow\orbr{\begin{cases}x-2=1\\x-2=-1\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}}\)

c) \(\left(2x-1\right)^2=-8\)

\(\Leftrightarrow2x-1=-2\)

\(\Leftrightarrow2x=-1\)

\(\Leftrightarrow x=-\frac{1}{2}\)

d) \(\left(x+\frac{1}{2}\right)^2=\frac{1}{16}\)

\(\Rightarrow\orbr{\begin{cases}x+\frac{1}{2}=\frac{1}{4}\\x+\frac{1}{2}=-\frac{1}{4}\end{cases}\Rightarrow\orbr{\begin{cases}x=-\frac{1}{4}\\x=-\frac{3}{4}\end{cases}}}\)

WT

what the fack

11 tháng 2 2018 - olm

tìm giá trị các biểu thức sau:1/ 3x44+5x22y22+2y44+2y22 biết rằng x22+y22=12/ 7x-7y+4ax-4ay-5 biết x-y=03/ x33+xy22-x22y-y33+3 biết x-y=04/ x22+2xy+y22-4x-4y+1 biết rằng x+y=3 giup voi mk dang...

#Hỏi cộng đồng OLM #Toán lớp 7

1

NT

Nhân Thiện Hoàng

11 tháng 2 2018

khó thể xem trên mạng

NV

Nguyễn Văn Tuấn

5 tháng 7 2018 - olm

Tìm x,y,x biết rằng:

(x-\(\frac{1}{2}\))(y+\(\frac{1}{3}\))(z-2)=0 và x+2=y+3=z+4

#Hỏi cộng đồng OLM #Toán lớp 7

2

HT

Hiếu Thông Minh

5 tháng 7 2018

(x-\(\frac{1}{2}\) )(y+\(\frac{1}{3}\) )(z-2)=0 và x+2=y+3=z+4

<=> x-\(\frac{1}{2}\)=0 hoặc y+\(\frac{1}{3}\)=0 hoặc z-2=0

+,với z-2=0

=>z=2

=>x+2=y+3=2+4

=>x+2=y+3=6

=. x=4;y=3

+,x-\(\frac{1}{2}\)=0

=>x=\(\frac{1}{2}\)

=>\(\frac{1}{2}\)+2=y+3=z+4

=>\(\frac{5}{2}\)=y+3=z+4

=>y=\(\frac{-1}{2}\);z=\(\frac{-3}{2}\)

+,với y+\(\frac{1}{3}\)=0

=>y=\(\frac{-1}{3}\)

=>x+2=\(\frac{-1}{3}\)+3=z+4

=>x+2=\(\frac{8}{3}\)=z+4

=>x=\(\frac{2}{3}\);z=\(\frac{4}{3}\)

Vậy khi x-\(\frac{1}{2}\)=0 thì x=\(\frac{1}{2}\);y=\(\frac{-1}{2}\);z=\(\frac{-3}{2}\)

khi y+\(\frac{1}{3}\)=0 thì x=\(\frac{2}{3}\);y=\(\frac{-1}{3}\);z=\(\frac{4}{3}\)

khi z-2=0 thì x=4;y=3;z=2

NV

Nguyễn Văn Tuấn

5 tháng 7 2018

Hiếu Thông Minh ơi giúp mình câu hỏi mình vừa đăng nữa nhé cảm ơn bạn mình sẽ k nhiều cho bạn !!!!!!!!

SG

Sách Giáo Khoa

10 tháng 5 2017

Tìm \(x\in\mathbb{Q}\), biết rằng :

a) \(\left(x-\dfrac{1}{2}\right)^2=0\)

b) \(\left(x-2\right)^2=1\)

c) \(\left(2x-1\right)^3=-8\)

d) \(\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{16}\)

#Hỏi cộng đồng OLM #Toán lớp 7

2

TN

Trần Ngọc Bích Vân

10 tháng 6 2017

a) \(\left(x-\dfrac{1}{2}\right)^2=0\Rightarrow x-\dfrac{1}{2}=0\Rightarrow x=\dfrac{1}{2}\)

b) Vì \(\left(x-2\right)^2=1\Rightarrow\left\{{}\begin{matrix}x-2=2\\x-2=-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=4\\x=0\end{matrix}\right.\)

Vậy x = 4 hoặc x = 0

c) Vì \(\left(2.x-1\right)^3=-8\Rightarrow2.x-1=-2\Rightarrow2.x=-1\Rightarrow x=-\dfrac{1}{2}\)

d) Vì \(\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{16}\Rightarrow\left\{{}\begin{matrix}x+\dfrac{1}{2}=\dfrac{1}{4}\\x+\dfrac{1}{2}=-\dfrac{1}{4}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{4}\\x=-\dfrac{3}{4}\end{matrix}\right.\)

MP

Mysterious Person

23 tháng 6 2017

a) \(\left(x-\dfrac{1}{2}\right)^2=0\Leftrightarrow x-\dfrac{1}{2}=0\Leftrightarrow x=\dfrac{1}{2}\)

b) \(\left(x-2\right)^2=1\Leftrightarrow\left\{{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)

c) \(\left(2x-1\right)^3=-8\Leftrightarrow2x-1=-2\Leftrightarrow2x=-1\Leftrightarrow x=\dfrac{-1}{2}\) d) \(\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{16}\Leftrightarrow x+\dfrac{1}{2}=\dfrac{1}{4}\Leftrightarrow x=\dfrac{-1}{4}\)

LN

LÊ NGỌC LINH

20 tháng 8 2017 - olm

Tìm x thuộc Q biết rằng:

a) \(\frac{11}{12}\)-(\(\frac{2}{5}\)+ x) =\(\frac{2}{3}\)

b) 2x. (x - \(\frac{1}{7}\))=0

c)\(\frac{3}{4}\)+ \(\frac{1}{4}\): x =\(\frac{2}{5}\)

#Hỏi cộng đồng OLM #Toán lớp 7

0

M

Min

25 tháng 2 2020 - olm

Tìm x ; y biết rằng :

a,\(\frac{x}{5}=\frac{y}{3}\)và x\(^2\)- y\(^2\)= 20 ( x ; y > 0 )

b, \(\frac{x^2}{y^2}=\frac{4}{9}\)và x\(^2\) . y\(^2\)= 576

#Hỏi cộng đồng OLM #Toán lớp 7

0

TN

Toàn Nguyễn

14 tháng 7 2016 - olm

Tìm x thuộc Q, biết rằng:

a) \(\left(x-\frac{1}{2}\right)^2=0\)

b) \(\left(x-2\right)^2=1\)

c) \(\left(2x-1\right)^3=-8\)

d) \(\left(x+\frac{1}{2}\right)^2=\frac{1}{16}\)

#Hỏi cộng đồng OLM #Toán lớp 7

2

OI

o0o I am a studious person o0o

14 tháng 7 2016

a) \(\left(x-\frac{1}{2}\right)^2=0\)

\(\Rightarrow\orbr{\begin{cases}x=\frac{-1}{2}\\x=\frac{1}{2}\end{cases}}\)

b) \(\left(x-2\right)^2=1\)

\(\Leftrightarrow\left(x-2\right)^2-1=0\)

\(\Leftrightarrow\left(x-2-1\right)\left(x-2+1\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}}\)

c) \(\left(2x-1\right)^3=-8\)

\(\Leftrightarrow2x-1=-2\)

\(\Leftrightarrow2x=-1\)

\(\Leftrightarrow x=\frac{-1}{2}\)

d) \(\left(x+\frac{1}{2}\right)^2=\frac{1}{16}\)

\(\Rightarrow x+\frac{1}{2}=\frac{1}{4}\)

\(\Rightarrow x=-\frac{1}{4}\)

K

kakashi

14 tháng 7 2016

a>(x-1/2)^2=0

(x-1/2)^2=0^2

=>x-1/2=0

x=1/2

b>(x-2)^2=1

(x-2)^2=1^2

=>x-2=1

x=3

(2x-1)^3=-8

=>(2x-1)^3=-2^3

=>2x-1=-2

2x=-1

x=-0,5

d>(x+1/2)^2=1/16

(x+1/2)^2=(1/4)^2

=>x+1/2=1/4

x=1/4-1/2

x=-1/4

chuc ban may man trong cuoc song!!!!!

NT

Nguyễn Thị Đỗ Quyên

14 tháng 7 2019 - olm

bài 1: tìm x biết rằng:

a. \(x^3=-27\) b.\(\left(2x-1\right)^3=8\) c.\(x^3=x^5\) d.\(\left(x-2\right)^2=16\) g.\(\left(2x-3\right)^2=9\) y.\(3x^3-4x=0\)

#Hỏi cộng đồng OLM #Toán lớp 7

1

K

KAl(SO4)2·12H2O

14 tháng 7 2019

a) x³ = -27

<=> -3³ = -27

=> x = -3

b) (2x - 1)³ = 8

<=> 8x³ - 12x² + 6x - 1 = 8

<=> 8x³ - 12x² + 6x - 1 - 8 = 0

<=> (2x - 3)(4x² + 3) = 0

<=> 2x - 3 = 0 hoặc 4x² + 3 = 0

2x = 0 + 3

2x = 3

x = 3/2

=> x = 3/2

c) x³ = x⁵

<=> x³ - x⁵ = 0

<=> x³(1 - x²) = 0

<=> x = 0; 1; -1

=> x = 0; 1; -1

d) (x - 2)² = 16

<=> (x - 2)² = 4²

<=> x - 2 = 4 hoặc x - 2 = -4

x = 4 + 2 x = -4 + 2

x = 6 x = -2

=> x = 6; -2

g) (2x - 3)² = 9

<=> (2x - 3)² = 3²

<=> 2x - 3 = 3 hoặc 2x - 3 = -3

2x = 3 + 3 2x = -3 + 3

2x = 6 2x = 0

x = 3 x = 0

=> x = 3; 0

y) 3x³ - 4x = 0

<=> x(3x - 4) = 0

<=> x = 0 hoặc 3x - 4 = 0

3x = 0 + 4

3x = 4

x = 4/3