
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(7x^{n-3}:\left(-8x^5\right)=-\dfrac{7}{8}x^{n-3-5}=-\dfrac{7}{8}x^{n-8}\)
Để đây là phép chia hết thì n-8>=0
hay n>=8
b: \(\dfrac{\left(3x^{n+1}-2x^5\right)}{-5x^3}=-\dfrac{3}{5}x^{n+1-3}+\dfrac{2}{5}x^2=\dfrac{-3}{5}x^{n-2}+\dfrac{2}{5}x^2\)
Để đây là phép chia hết thì n-2>=0
hay n>=2

1: \(\dfrac{A}{B}=\dfrac{4}{3}x^{n+1-3}y^{2-n+1}=\dfrac{4}{3}x^{n-2}y^{3-n}\)
Để A chia hết cho B thì \(\left\{{}\begin{matrix}n-2>=0\\3-n< =0\end{matrix}\right.\Leftrightarrow2< =n< =3\)
2: \(\dfrac{A}{B}=\dfrac{7}{5}x^{n-1-2}y^{5-n}-xy^{4-n}=\dfrac{7}{5}x^{n-3}y^{5-n}-xy^{4-n}\)
Để A chia hết cho B thì \(\left\{{}\begin{matrix}n-3>=0\\5-n>=0\\4-n>=0\end{matrix}\right.\Leftrightarrow3\le n\le4\)
(\(\frac{3}{4}\)x n+1 - \(\frac{1}{2}\)yn) .2xy - (\(\frac{2}{3}\)xn+1 - \(\frac{5}{6}\)yn ).7xy
\(\)

giúp mik bài này với :
tìm giá trị lớn nhất của A=x-x-1
giúp mik nha
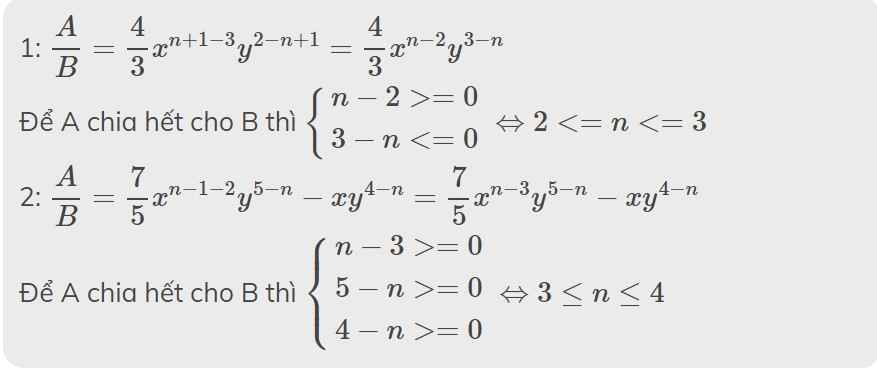
 N để:
N để: