K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 9 2016
a)(|x-2|-3)(5+|x|)=0
<=>|x-2|-3=0 hoặc 5+|x|=0
*)Xét |x-2|-3=0 <=>|x-2|=3
=>x-2=±3
Với x-2=3 =>x=5
Với x-2=-3 =>x=-1
*)Xét 5+|x|=0
=>|x|=-5 (mà \(\left|x\right|\ge0>-5\) với mọi x)
=>vô nghiệm
14 tháng 9 2016
(2x-1)2=1-2x
<=>4x2-4x+1=1-2x
<=>4x2-2x=0
<=>2x(2x-1)=0
<=>x=0 hoặc x=\(\frac{1}{2}\)
NT
0
UT
2
6 tháng 10 2019
\(5^{x-1}+2=127\)
\(\Leftrightarrow5^{x-1}=125\)\(=5^3\)
\(\Rightarrow x-1=3\Rightarrow x=4\)
11 tháng 8 2016
Do \(\left|2x+3\right|=x+2\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}2x+3=x+2\\2x+3=-\left(x+2\right)\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}2x-x=2-3\\2x+3=-x-2\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-1\\2x+x=-2-3\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-1\\3x=-5\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-1\\x=-\frac{5}{3}\end{array}\right.\)
11 tháng 8 2016
\(\left|2x+3\right|=x+2\) (1)
+)TH1: \(2x+3\ge0\Rightarrow x\ge-\frac{3}{2}\) yhif pt (1) trở thành
\(2x+3=x+2\Leftrightarrow x=-1\left(Tm\right)\)
+)TH2: \(2x+3< 0\Leftrightarrow x< -\frac{3}{2}\) thi pt (1) trở thành
\(-2x-3=x+2\Leftrightarrow-3x=5\Leftrightarrow x=-\frac{5}{3}\) (TM)
NT
2
18 tháng 9 2016
Ta có : \(\frac{x}{4}=\frac{y}{2}=\frac{z}{5}\) và \(2y^2+z^2-x^2=17\)
Áp dụng tính chất của dãy tỉ số bằng nhau , ta có :
\(\frac{x}{4}=\frac{y}{2}=\frac{z}{5}=\frac{2y^2+z^2-x^2}{2.2^2+5^2-4^2}=\frac{17}{17}=1\)
\(\Rightarrow\begin{cases}\frac{x}{4}=1\Rightarrow x=1.4=4\\\frac{y}{2}=1\Rightarrow y=2.1=2\\\frac{z}{5}=1\Rightarrow z=5.1=5\end{cases}\)
Vậy .................
18 tháng 9 2016
\(\frac{x}{4}=\frac{y}{2}=\frac{z}{5}\)
=> \(\frac{x^2}{16}=\frac{2y^2}{8}=\frac{z^2}{25}\)
Áp dụng tính chất của dãy tỉ số = nhau ta có:
\(\frac{x^2}{16}=\frac{2y^2}{8}=\frac{z^2}{25}=\frac{2y^2+z^2-x^2}{8+25-16}=\frac{17}{17}=1\)
=> \(\begin{cases}x^2=1.16=16\\y^2=1.8:2=4\\z^2=1.25=25\end{cases}\) => \(\begin{cases}x\in\left\{4;-4\right\}\\y\in\left\{2;-2\right\}\\z\in\left\{5;-5\right\}\end{cases}\)
Vậy \(\begin{cases}x=4\\y=2\\z=5\end{cases}\); \(\begin{cases}x=-4\\y=-2\\z=-5\end{cases}\)
NT
2
29 tháng 7 2016
\(\frac{x-1}{x+2}=\frac{x-2}{x+3}\)
\(\Rightarrow\left(x-1\right)\left(x+3\right)=\left(x-2\right)\left(x+2\right)\)
\(\Rightarrow x^2+2x-3=x^2-4\)
\(\Rightarrow x^2+2x-x^2=-4+3\) ( qui tắc chuyển vế )
\(\Rightarrow2x=-1\)
\(\Rightarrow x=-\frac{1}{2}\)
15 tháng 9 2016
\(n^{150}< 5^{225}\)
\(\Rightarrow n^{150}=\left(n^2\right)^{75}\)
\(\Leftrightarrow\left(n^2\right)^{75}< \left(5^3\right)^{75}\)
\(\Rightarrow n^2< 125\)
\(\Rightarrow n< 12\)
\(\left|x-3,5\right|+\left|4,5-x\right|=0\)
\(\Rightarrow\left|x-3,5\right|=\left|4,5-x\right|\)
\(\Rightarrow x-3,5=4,5-x\)
\(\Rightarrow x+x=4,5+3,5\)
\(\Rightarrow2x=8\)
\(\Rightarrow x=4\)
17 tháng 12 2016
\(\frac{x+11}{12}+\frac{x+11}{13}+\frac{x+11}{14}=\frac{x+11}{15}+\frac{x+11}{16}\)
\(\Rightarrow\frac{x+11}{12}+\frac{x+11}{13}+\frac{x+11}{14}-\frac{x+11}{15}-\frac{x+11}{16}=0\)
\(\Rightarrow\left(x+11\right)\left(\frac{1}{12}+\frac{1}{13}+\frac{1}{14}-\frac{1}{15}-\frac{1}{16}\right)=0\)
Mà \(\left(\frac{1}{12}+\frac{1}{13}+\frac{1}{14}-\frac{1}{15}-\frac{1}{16}\right)\ne0\)
\(\Rightarrow x+11=0\Rightarrow x=-11\)
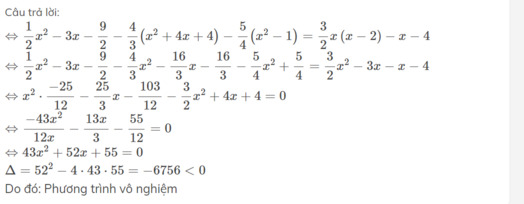
\(|x|=\frac{1}{5}\)
=> \(\orbr{\begin{cases}x=\frac{1}{5}\\x=-\frac{1}{5}\end{cases}}\)
\(x=\frac{1}{5}\)\(;-\frac{1}{5}\)