
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

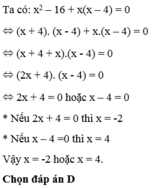

\(2x\left(x-3\right)+5\left(x-3\right)=0\)
\(\Leftrightarrow\left(2x+5\right)\left(x-3\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}2x+5=0\\x-3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{-5}{2}\\x=3\end{cases}}\)
Chọn ( B )

\(a)\) \(3-2x>4x+5\)
\(\Leftrightarrow\)\(3-2x+2x>4x+2x+5\)
\(\Leftrightarrow\)\(6x+5< 3\)
\(\Leftrightarrow\)\(6x+5-5< 3-5\)
\(\Leftrightarrow\)\(6x< -2\)
\(\Leftrightarrow\)\(\frac{6x}{6}< \frac{-2}{6}\)
\(\Leftrightarrow\)\(x< \frac{-1}{3}\)
Vậy \(x< \frac{-1}{3}\)
Chúc bạn học tốt ~

Đặt \(|x-4|=t\)
Khi đó: \(C=t\left(2-t\right)\)
\(=2t-t^2\)
\(=-t^2+2t-1+1\)
\(=-\left(t^2-2t+1\right)+1\)
\(=-\left(t-1\right)^2+1\le1\forall t\)
Dấu "=" xảy ra khi:
\(t-1=0\Rightarrow t=1\Rightarrow|x-4|=1\Rightarrow\orbr{\begin{cases}x-4=1\\x-4=-1\end{cases}\Rightarrow\orbr{\begin{cases}x=5\\x=3\end{cases}}}\)
Vậy GTLN của C là 1 khi \(\orbr{\begin{cases}x=5\\x=3\end{cases}}\)
Chúc bạn học tốt.

1: (x2-4x+3)=(x-1)(x-3) lớn hơn or bằng 0
suy ra: x<=1 hoặc 3<=x
2: x3-2x2+3x-6=(x-2)(x2+3)<0
mà x2+3>0 =>x<2
3: x+2 lớn hơn hoặc bằng 0 => x lớn hơn hoặc bằng -2
4: =>x+2>0 và x-3<0 => -2<x<3
1, \(x^2-4x+3\ge0\Leftrightarrow\left(x-3\right)\left(x-1\right)\ge0\)
TH1 : \(\hept{\begin{cases}x-3\ge0\\x-1\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge3\\x\ge1\end{cases}\Leftrightarrow}x\ge3}\)
TH2 : \(\hept{\begin{cases}x-3\le0\\x-1\le0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le3\\x\le1\end{cases}\Leftrightarrow}x\le1}\)
Vậy BFT có tập nghiệm là S = { x | x =< 1 ; x >= 3 }
2, \(x^3-2x^2+3x-6< 0\Leftrightarrow x^2\left(x-2\right)+3\left(x-2\right)< 0\)
\(\Leftrightarrow\left(x^2+3\right)\left(x-2\right)< 0\Rightarrow x-2< 0\)vì \(x^2+3>0\forall x\)
\(\Leftrightarrow x< 2\)Vậy BFT có tập nghiệm là S = { x | x < 2 }

a) \(9x^2+6x+1=\left(3x\right)^2+2.3x.1+1^2=\left(3x+1\right)^2\)
b) \(x^2-x+\dfrac{1}{4}=x^2-2.\dfrac{1}{2}x+\left(\dfrac{1}{2}\right)^2=\left(x-0,5\right)^2\)
c) \(x^2y^4-2xy^2+1=\left(xy^2\right)^2-2.xy^2.1+1^2=\left(xy^2-1\right)^2\)
d) \(x^2+\dfrac{2}{3}x+\dfrac{1}{9}=x^2+2.x.\dfrac{1}{3}+\left(\dfrac{1}{3}\right)^2=\left(x+\dfrac{1}{3}\right)^2\)
a) \(9x^2+6x+1\)
\(=\left(3x\right)^2+2.3x.1+1^2\)
\(=\left(3x+1\right)^2\)