Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
\(\dfrac{1}{2}\)(\(\dfrac{1}{1}\)-\(\dfrac{1}{3}\)+\(\dfrac{1}{3}\)-\(\dfrac{1}{5}\)+\(\dfrac{1}{5}\)-\(\dfrac{1}{7}\)+...+\(\dfrac{1}{x}\)-\(\dfrac{1}{x+2}\))=\(\dfrac{20}{41}\)
\(\dfrac{1}{2}\)(\(\dfrac{1}{3}\)-\(\dfrac{1}{x+2}\))=\(\dfrac{20}{41}\)
\(\dfrac{1}{3}\)-\(\dfrac{1}{x+2}\)=\(\dfrac{40}{41}\)
\(\dfrac{1}{x+2}\)=\(\dfrac{1}{3}\)-\(\dfrac{40}{41}\)

\(A=\dfrac{2^2}{1.3}+\dfrac{3^2}{2.4}+\dfrac{4^2}{3.5}+\dfrac{5^2}{4.6}+\dfrac{6^2}{5.7}\)
\(A=\dfrac{2.2.3.3.4.4.5.5.6.6}{1.3.2.4.3.5.4.6.5.7}\)
\(A=\dfrac{2.3.4.5.6}{1.2.3.4.5}.\dfrac{2.3.4.5.6}{3.4.5.6.7}\)
\(A=\dfrac{6}{1}.\dfrac{2}{7}=\dfrac{12}{7}\)
\(B=\left(1+\dfrac{1}{1.3}\right)\left(1+\dfrac{1}{2.4}\right)\left(1+\dfrac{1}{3.5}\right)\left(1+\dfrac{1}{9.11}\right)\)
\(B=\dfrac{4}{3}.\dfrac{9}{8}.\dfrac{16}{15}.\dfrac{100}{99}\)
\(B=\dfrac{4.9.16.100}{3.8.15.99}\)
\(B=\dfrac{2.2.3.3.4.4.10.10}{1.3.2.4.3.5.9.11}\)
\(B=\dfrac{2.3.4.10}{1.2.3.9}.\dfrac{2.3.4.10}{3.4.5.11}\)
\(B=10.\dfrac{2}{11}=\dfrac{20}{11}\)

Ta có: \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{x\left(x+2\right)}=\dfrac{20}{41}\)
\(\Leftrightarrow\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{x\left(x+2\right)}=\dfrac{40}{41}\)
\(\Leftrightarrow1-\dfrac{2}{x+2}=\dfrac{40}{41}\)
\(\Leftrightarrow\dfrac{2}{x+2}=\dfrac{1}{41}\)
Suy ra: x+2=82
hay x=80

b,\(\dfrac{1}{3.5}+\dfrac{1}{5.7}\)\(+\dfrac{1}{7.9}+....+\dfrac{1}{\left(2x+1\right).\left(2x+3\right)}=\dfrac{15}{93}\)
\(\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{2x+1}-\dfrac{1}{2x+3}\right).\dfrac{1}{2}=\dfrac{15}{93}\)
\(\left[\dfrac{1}{3}+\left(\dfrac{1}{5}-\dfrac{1}{5}\right)+\left(\dfrac{1}{7}-\dfrac{1}{7}\right)+....+\left(\dfrac{1}{2x+1}-\dfrac{1}{2x+1}\right)-\dfrac{1}{2x+3}\right].\dfrac{1}{2}=\dfrac{15}{93}\)
\(\left(\dfrac{1}{3}+0+0+...+0-\dfrac{1}{2x+3}\right).\dfrac{1}{2}=\dfrac{15}{93}\)
\(\dfrac{1}{3}-\dfrac{1}{2x+3}=\dfrac{15}{93}:\dfrac{1}{2}\)
\(\dfrac{1}{3}-\dfrac{1}{2x+3}=\dfrac{10}{31}\)
\(\dfrac{1}{2x+3}=\dfrac{1}{3}-\dfrac{10}{31}\)
\(\dfrac{1}{2x+3}=\dfrac{1}{93}\)
\(\Rightarrow2x+3=93\)
\(2x=93-3=90\)
\(\Rightarrow x=90:2=45\)

\(P=\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{\left(2n+1\right)\left(2n+3\right)}\\ 2P=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{\left(2n+1\right)\left(2n+3\right)}\\ =\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2n+1}-\dfrac{1}{2n+3}\\ =1-\dfrac{1}{2n+3}\\ =\dfrac{2\left(n+1\right)}{2n+3}\\ P=\dfrac{2\left(n+1\right)}{2n+3}:2\\ =\dfrac{n+1}{2n+3}\)
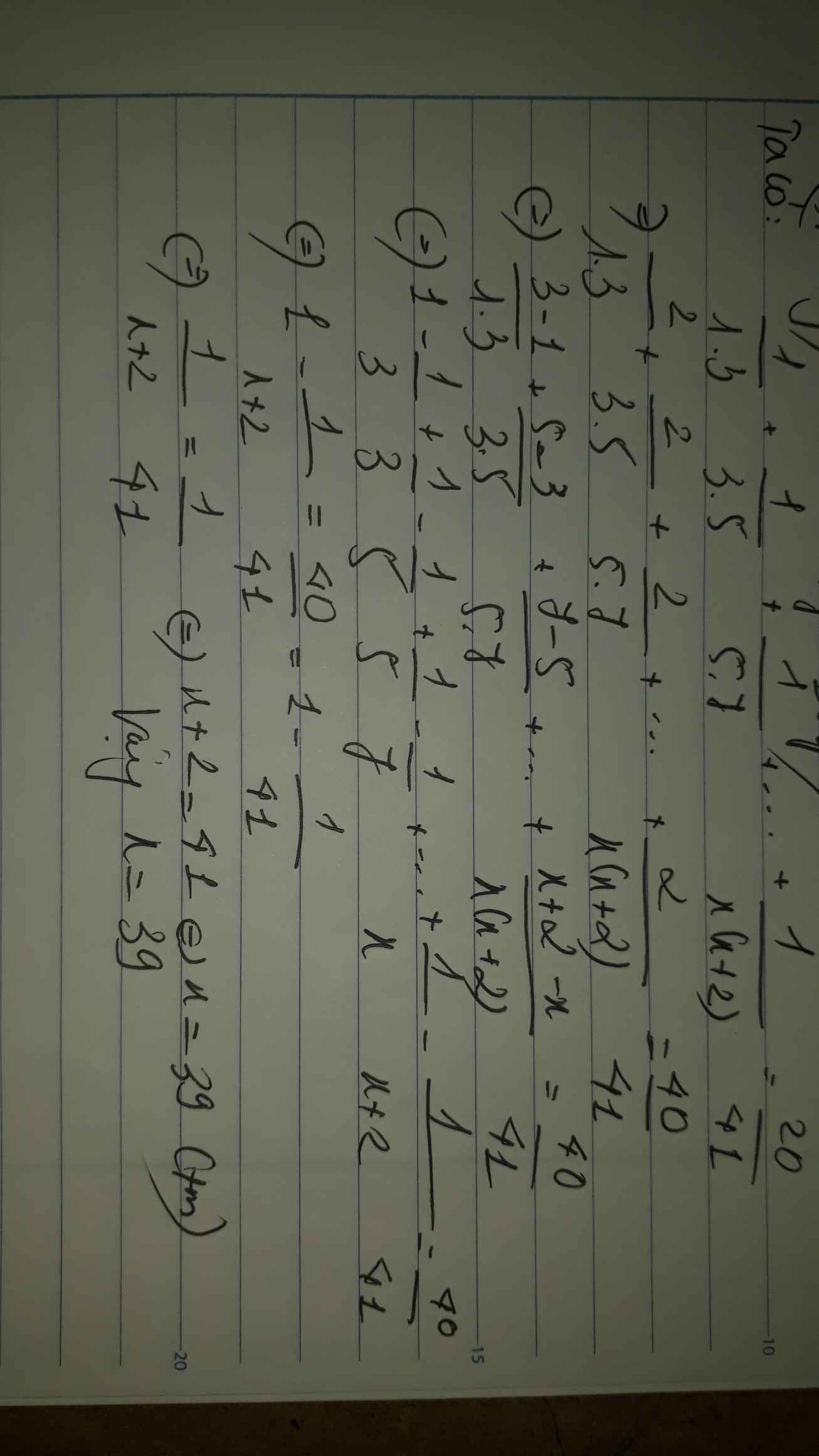
\(\dfrac{1}{1.3}\)+ \(\dfrac{1}{3.5}\)+ \(\dfrac{1}{5.7}\)+....+\(\dfrac{1}{x\left(x+1\right)}\) = \(\dfrac{1005}{2011}\)
1- \(\dfrac{1}{3}\)+ \(\dfrac{1}{3}\) - \(\dfrac{1}{5}\)+ \(\dfrac{1}{5}\)- \(\dfrac{1}{7}\)+....+\(\dfrac{1}{x}\)- \(\dfrac{1}{x+1}\)= \(\dfrac{1005}{2011}\)
1- \(\dfrac{1}{x+1}\)= \(\dfrac{1005}{2011}\)
\(\dfrac{1}{x+1}\)= 1- \(\dfrac{1005}{2011}\)
\(\dfrac{1}{x+1}\)= \(\dfrac{1006}{2011}\)
=> x +1= 2011
=> x= 2011-1
=> x=2010
Bài này mk lm đại nha bn ! Cs j sai mong bn bỏ qua
! Cs j sai mong bn bỏ qua  .
.
ko biết