Tìm x, biết: 4 x 2 +...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

26 tháng 2 2018

Tìm x, biết: 4 x 2 + 4 x + 1 = 6

#Hỏi cộng đồng OLM #Toán lớp 9

1

CM

Cao Minh Tâm

26 tháng 2 2018

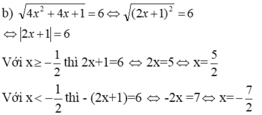
Để học tốt Toán 9 | Giải bài tập Toán 9

Các câu hỏi dưới đây có thể giống với câu hỏi trên

TH

Trần Huỳnh Như

3 tháng 8 2016

Tìm x biết

a/\(\sqrt{x^2+x+\frac{1}{4}}-\sqrt{4-2\sqrt{3}=0}\)

b/\(x-5\sqrt{x}+6=0\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

TV

Trần Việt Linh

3 tháng 8 2016

a)\(\sqrt{x^2+x+\frac{1}{4}}-\sqrt{4-2\sqrt{3}}=0\)

\(\Leftrightarrow\sqrt{\left(x+\frac{1}{2}\right)^2}-\sqrt{\left(\sqrt{3}-1\right)^2}=0\)

\(\Leftrightarrow x+\frac{1}{2}-\sqrt{3}+1=0\)

\(\Leftrightarrow x=\sqrt{3}-1-\frac{1}{2}\)

\(\Leftrightarrow x=\sqrt{3}-\frac{3}{2}\)

b)\(x-5\sqrt{x}+6=0\)

\(\Leftrightarrow x-2\sqrt{x}-3\sqrt{x}+6=0\)

\(\Leftrightarrow\sqrt{x}\left(\sqrt{x}-2\right)-3\left(\sqrt{x}-2\right)=0\)

\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)=0\)

\(\Leftrightarrow\left[\begin{array}{nghiempt}\sqrt{x}-2=0\\\sqrt{x}-3=0\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}\sqrt{x}=2\\\sqrt{x}=3\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}x=4\\x=9\end{array}\right.\)

VT

Vũ Thị Ngọc Chi

6 tháng 10 2017 - olm

1. Cho A=\(\frac{3}{2+\sqrt{2x-x^2}+3}\)a. Tìm x để A có nghĩab. Tìm Min(A), Max(A)2/ Tìm Min, Max của: \(A=\frac{1}{2+\sqrt{x-x^2}}\)3/ Tìm Min(B) biết: \(B=\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\)4/ Tìm Min, Max của:\(C=\frac{4x+3}{x^2+1}\)5/ Tìm Max của: \(A=\sqrt{x-1}+\sqrt{y-2}\)biết \(x+y=4\)6/ Tìm Max(B) biết: \(B=\frac{y\sqrt{x-1}+x\sqrt{y-2}}{xy}\)7/ Tìm Max(C)...

#Hỏi cộng đồng OLM #Toán lớp 9

2

OS

oOo Sát thủ bóng đêm oOo

28 tháng 7 2018

tích mình với

ai tích mình

mình tích lại

thanks

NT

Nguyễn Thế Công

14 tháng 2 2019

Tích mình đi mình tích lại

ND

Nguyễn Đức Anh

27 tháng 5 2015 - olm

Tìm Min A, biết \(A=\left(x-1\right)^4+\left(x-3\right)^4+6\left(x-1\right)^2\left(x-3\right)^2\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

TT

Trần Thị Loan

27 tháng 5 2015

Đặt a = x - 2 => x - 1 = a + 1; x - 3 = a -1

Khi đó, A = (a+1)⁴ + (a - 1)⁴ + 6.(a + 1)² .(a - 1)²

A = [(a + 1)² + (a - 1)²]² + 4.(a + 1)² .(a - 1)²

= (a² + 2a + 1 + a² - 2a + 1)² + 4.(a² - 1)²

= (2a² +2)² + 4.(a⁴ - 2a² + 1)

= 4a⁴ + 8a² + 4 + 4a⁴ - 8a² + 4 = 8a⁴ + 8 \(\ge\) 8 với mọi a

=> min A = 8 khi a = 0 <=> x - 2 = 0 <=> x= 2

TH

Tô Hoài Dung

15 tháng 10 2016 - olm

Tìm x biết \(\sqrt{x-2+2\sqrt{x-3}}+\sqrt{x+6+6\sqrt{x-3}}=4\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

HL

Hoàng Lê Bảo Ngọc

15 tháng 10 2016

ĐKXĐ : \(x\ge3\)

\(\sqrt{x-2+2\sqrt{x-3}}+\sqrt{x+6+6\sqrt{x-3}}=4\)

\(\Leftrightarrow\sqrt{\left(\sqrt{x-3}+1\right)^2}+\sqrt{\left(\sqrt{x-3}+3\right)^2}=4\)

\(\Leftrightarrow\sqrt{x-3}+1+\sqrt{x-3}+3=4\)

\(\Leftrightarrow2\sqrt{x-3}=0\Leftrightarrow x=3\)(TMĐK)

IT

ʚĭɞ Thị Quyên ʚĭɞ

28 tháng 8 2016

tìm x, y, z biết x+y+z+8=\(2\sqrt{x-1}+4\sqrt{y-2}+6\sqrt{z-3}\)

#Hỏi cộng đồng OLM #Toán lớp 9

0

LT

Lê Tài Bảo Châu

2 tháng 8 2020 - olm

Bài 1: Cho \(x,y>0\)thỏa mãn \(x^4+y^4=4\).Tìm GTNN \(E=\left(x+\frac{1}{y}\right)^2+\left(y+\frac{1}{x}\right)^2\)Bài 2: Tìm GTNN và GTLN của\(A=\sqrt{3+x}+\sqrt{6-x}\left(-3\le x\le6\right)\)Bài 3:Tìm GTLN...

#Hỏi cộng đồng OLM #Toán lớp 9

6

K

KP9

2 tháng 8 2020

Bài 2 :

Tìm min : Bình phương

Tìm max : Dùng B.C.S ( bunhiacopxki )

Bài 3 : Dùng B.C.S

LT

Lê Tài Bảo Châu

2 tháng 8 2020

KP9

nói thế thì đừng làm cho nhanh bạn ạ

Người ta cũng có chút tôn trọng lẫn nhau nhé đừng có vì dăm ba cái tích

MY

Min YoongMin

24 tháng 6 2019 - olm

Tìm x, biết:

a. \(\sqrt{6-4x+x^2}-x=4\)

b. \(\sqrt{4x^2-4x+1}+\sqrt{2x-1}=0\)với \(x\ge\frac{1}{2}\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

G

Girl

24 tháng 6 2019

a) ĐKXĐ: \(x\ge-4\)

a) Ta có: \(\sqrt{6-4x+x^2}=x+4\Rightarrow\left(x+4\right)^2=x^2-4x+6\)

\(\Rightarrow x^2+8x+16=x^2-4x+6\Rightarrow4x+10=0\Rightarrow x=-\frac{5}{2}\left(loại\right)\)

Vậy pt vô nghiệm

b) \(\sqrt{4x^2-4x+1}+\sqrt{2x-1}=0\Rightarrow\sqrt{\left(2x-1\right)^2}+\sqrt{2x-1}=0\)

\(\Leftrightarrow\sqrt{2x-1}\left(\sqrt{2x-1}+1\right)=0\Rightarrow x=\frac{1}{2}\)

G

gh

18 tháng 10 2020 - olm

tìm x biết

a) \(\sqrt{x+1}=2\)

b)\(2\sqrt{x-2}< 6\)

c)\(\sqrt{x^2-16}=-\sqrt{x-4}\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

NN

Nobi Nobita

18 tháng 10 2020

a) \(ĐKXĐ:x\ge-1\)

\(\sqrt{x+1}=2\)\(\Rightarrow\left(\sqrt{x+1}\right)^2=4\)

\(\Rightarrow x+1=4\)\(\Leftrightarrow x=3\)( thỏa mãn ĐKXĐ )

Vậy \(x=3\)

b) \(ĐKXĐ:x\ge2\)

\(2\sqrt{x-2}< 6\)\(\Leftrightarrow\sqrt{x-2}< 3\)

Vì \(\sqrt{x-2}\ge0\); \(3>0\)

\(\Rightarrow\left(\sqrt{x-2}\right)^2< 9\)\(\Leftrightarrow x-2< 9\)

\(\Leftrightarrow x< 11\)

Kết hợp với ĐKXĐ \(\Rightarrow2\le x< 11\)

Vậy \(2\le x< 11\)

c) \(ĐKXĐ:x\ge4\)

\(\sqrt{x^2-16}=-\sqrt{x-4}\)

\(\Leftrightarrow\sqrt{x^2-16}+\sqrt{x-4}=0\)

\(\Leftrightarrow\sqrt{\left(x-4\right)\left(x+4\right)}+\sqrt{x-4}=0\)

\(\Leftrightarrow\sqrt{x-4}.\left(\sqrt{x+4}+1\right)=0\)

Vì \(\sqrt{x+4}>0\)\(\Rightarrow\sqrt{x+4}+1>0\)

\(\Rightarrow\sqrt{x-4}=0\)\(\Leftrightarrow x-4=0\)\(\Leftrightarrow x=4\)

Vậy \(x=4\)

LT

Lê Thảo Linh

18 tháng 7 2015 - olm

Tìm x, biết: \(\sqrt{4\left(1-x\right)^2}\)-6 =0

#Hỏi cộng đồng OLM #Toán lớp 9

0

MT

Minh Triều

10 tháng 9 2015 - olm

Tìm x biết: \(\sqrt{4.\left(x-1\right)^2}-6=0\)

#Hỏi cộng đồng OLM #Toán lớp 9

4

NH

Nguyễn Huy Hải

10 tháng 9 2015

@@ bây giờ mới ngỡ ra

TH1:

2.|x-1| = 6

=> 2.(x-1) = 6

2x-2 = 6

2x = 6+2

x = 8

x = 8:2

x = 4

TH2:

2.|x-1| = 6

=> 2[-(x-1)] = 6

2.[-x+1] = 6

-2x+2 = 6

-2x = 6-2

-2x = 4

x = 4:(-2)

x = -2

TQ

Tạ Quang Duy

10 tháng 9 2015

=>\(\sqrt{4\left(X-1\right)^2}=6\Rightarrow4\left(X-1\right)^2=36\Rightarrow\left(X-1\right)^2=9\Rightarrow X-1=3\Rightarrow X=4\)