
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: 10x=6y=5z⇔x110=y16=z1510x=6y=5z⇔x110=y16=z15 và x+y−z=24x+y−z=24
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x110=y16=z15=x+y−z110+16−15=24:115=360x110=y16=z15=x+y−z110+16−15=24:115=360
=> x = 360 : 10 = 36
y = 360 : 6 = 60
z = 360 : 5 = 72
dựa theo lm nhá ! chúc học tốt

a) \(3.\left(10.x\right)=111\)
\(10.x=37\)
\(x=\dfrac{37}{10}\)
b) \(3.\left(10+x\right)=111\)
\(10+x=37\)
\(x=27\)
c) \(3+\left(10.x\right)=111\)
\(10.x=108\)
\(x=\dfrac{54}{5}\)
d) \(3+\left(10+x\right)=111\)
\(x=111-3-10\)
\(x=98\)

1.b) \(\left(\left|x\right|-3\right)\left(x^2+4\right)< 0\)
\(\Rightarrow\hept{\begin{cases}\left|x\right|-3\\x^2+4\end{cases}}\) trái dấu
\(TH1:\hept{\begin{cases}\left|x\right|-3< 0\\x^2+4>0\end{cases}}\Leftrightarrow\hept{\begin{cases}\left|x\right|< 3\\x^2>-4\end{cases}}\Leftrightarrow x\in\left\{0;\pm1;\pm2\right\}\)
\(TH1:\hept{\begin{cases}\left|x\right|-3>0\\x^2+4< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}\left|x\right|>3\\x^2< -4\end{cases}}\Leftrightarrow x\in\left\{\varnothing\right\}\)
Vậy \(x\in\left\{0;\pm1;\pm2\right\}\)

Đặt \(\frac{x}{2}=\frac{y}{3}=k\)\(\left(k\ne0\right)\)
=> x=2k , y =3k
x.y=54 => 2k.3k=54 => 6k^2=54
=> k=\(+-3\)
=> (x,y)=(6,9) = (-6,-9)

1, a/ \(\left|x\right|=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{-1}{2}\end{matrix}\right.\)
Vậy .............
b/ \(\left|x\right|=3,12\Leftrightarrow\left[{}\begin{matrix}x=3,12\\x=-3,12\end{matrix}\right.\)
Vậy ...........
c/ \(\left|x\right|=0\Leftrightarrow x=0\)
Vậy ..........
d/ \(\left|x\right|=2\dfrac{1}{7}\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\dfrac{1}{7}\\x=-2\dfrac{1}{7}\end{matrix}\right.\)
Vậy ..............
2, a/ \(\left|x\right|=2,1\Leftrightarrow\left[{}\begin{matrix}x=2,1\\x=-2,1\end{matrix}\right.\)
Vậy ...........
b/ \(\left|x\right|=\dfrac{17}{9}\) ; \(x< 0\)
\(\Leftrightarrow x=-\dfrac{17}{9}\)
Vậy ..........
c/ \(\left|x\right|=1\dfrac{2}{5}\Leftrightarrow\left[{}\begin{matrix}x=1\dfrac{2}{5}\\x=-1\dfrac{2}{5}\end{matrix}\right.\)
Vậy ...........
d/ \(\left|x\right|=0,35\) ; \(x>0\Leftrightarrow x=0,35\)
3, a/ \(\left|x-1,7\right|=2,3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1,7=2,3\\x-1,7=-2,3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-0,6\end{matrix}\right.\)
Vậy ...........
b/ \(\left|x+\dfrac{3}{4}\right|-\dfrac{1}{3}=0\)
\(\Leftrightarrow\left|x+\dfrac{3}{4}\right|=\dfrac{1}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{3}\\x+\dfrac{3}{4}=-\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-5}{12}\\x=-\dfrac{13}{12}\end{matrix}\right.\)
Vậy ...........

a) Ta có : \(\left|3x+4\right|=2\left|2x-9\right|\)
=> \(\orbr{\begin{cases}3x+4=2\left(-2x+9\right)\\3x+4=2\left(2x-9\right)\end{cases}}\Rightarrow\orbr{\begin{cases}3x+4=-4x+18\\3x+4=4x-18\end{cases}}\Rightarrow\orbr{\begin{cases}7x=14\\-x=-22\end{cases}}\Rightarrow\orbr{\begin{cases}x=2\\x=22\end{cases}}\)
=> \(x\in\left\{2;22\right\}\)
b) Ta có : \(\left|10x+7\right|< 37\)
=> -37 < 10x + 7 < 37
=> -44 < 10x < 30
=> -4,4 < x < 3
Vậy -4,4 < x < 3
c) |3 - 8x| \(\le\)19
=> \(-19\le3-8x\le19\)
=> \(\hept{\begin{cases}3-8x\ge-19\\3-8x\le19\end{cases}}\Rightarrow\hept{\begin{cases}22\ge8x\\-16\le8x\end{cases}}\Rightarrow\hept{\begin{cases}x\le\frac{11}{4}\\x\ge-2\end{cases}}\Rightarrow-2\le x\le\frac{11}{4}\)
d) Ta có |x + 3| - 2x = |x - 4| (1)
Nếu x < -3
=> |x + 3| = -(x + 3) = -x - 3
=> |x - 4| = -(x - 4) = -x + 4
Khi đó (1) <=> -x - 3 - 2x = - x + 4
=> -3x - 3 = - x + 4
=> -2x = 7
=> x = - 3,5 (tm)
Nếu \(-3\le x\le4\)
=> |x + 3| = x + 3
=> |x - 4| = -(x - 4) = -x + 4
Khi đó (1) <=> x + 3 - 2x = -x + 4
=> -x + 3 = -x + 4
=> 0x = 1 (loại)
Nếu x > 4
=> |x + 3| = x + 3
=> |x - 4| = x + 4
Khi đó (1) <=> x + 3 - 2x = x - 4
=> -x + 3 = x - 4
=> -2x = -7
=> x = 3,5 (loại)
Vậy x = -3,5

a) |x -1,7| = 2,3 => x - 1,7 = 2,3 hoặc x - 1,7 = -2,3
Với x - 1,7 = 2,3 => x = 4
Với x - 1,7 = -2,3 => x= -0,6
Vậy x = 4 hoặc x = -0,6
b) 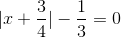 =>
=> 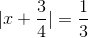
Suy ra: 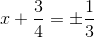
Với 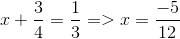
Với 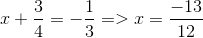

Bài 1:
a) \(x^2+5x+6=x^2+2x+3x+6=x\left(x+2\right)+3\left(x+2\right)=\left(x+2\right)\left(x+3\right)\)
b) \(2x^2+5x+3=2x^2+2x+3x+3=2x\left(x+1\right)+3\left(x+1\right)=\left(x+1\right)\left(2x+3\right)\)
c) \(x^2-10x+16=x^2-2x-8x+16=x\left(x-2\right)-8\left(x-2\right)=\left(x-2\right)\left(x-8\right)\)
d) \(4x^2+9x+5=4x^2+4x+5x+5=4x\left(x+1\right)+5\left(x+1\right)=\left(x+1\right)\left(4x+5\right)\)
Bài 2:
không rõ đề --> k lm

\(A=\frac{x^2-10x+36}{x-5}=\frac{x^2-10x+25+9}{x-5}\) \(=\frac{\left(x-5\right)^2+9}{x-5}=x-5+\frac{9}{x-5}\)
để \(A\in Z\)
<=> \(\frac{9}{x-5}\in Z\)mà \(x\in Z\)
=> \(x-5\inƯ\left(9\right)\)
=> \(x-5\in\left(1;-1;3;-3;9;-9\right)\)
=> \(x\in\left(6;4;8;2;14;-4\right)\)
học tốt
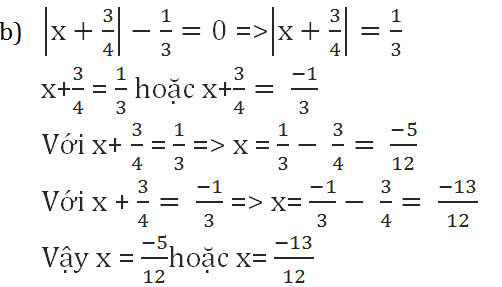
Ta có:
Chọn đáp án D