PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
0
HH
26 tháng 2 2020
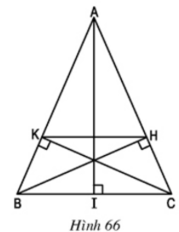
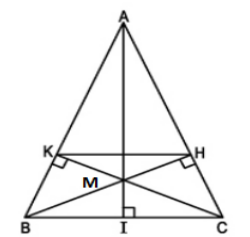
A B C K H I
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)
22 tháng 4 2017
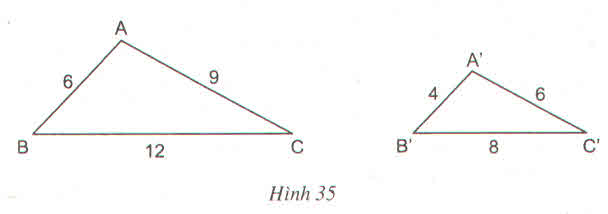
ABA′B′ABA′B′ = BCB′C′BCB′C′= CAC′A′CAC′A′= 3/2
=> ∆ABC ∽ ∆A'B'C'
b) CABCCA′B′C′CABCCA′B′C′= 3/2
HB
22 tháng 4 2017
a)Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có:
\(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}\)
\(\Rightarrow\Delta ABC\)∽\(\Delta A'B'C'\)(c.c.c)
b)Từ câu a và áp dụng tính chất tỉ lệ thức ta có:
\(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}=\dfrac{AB+BC+AC}{A'B'+B'C'+A'C'}=\dfrac{3}{2}\)
mà \(C_{ABC}=AB+BC+AC\)
\(C_{A'B'C'}=A'B'+B'C'+A'C'\)
Vậy tỉ số chu vi của \(\Delta ABC\) và \(\Delta A'B'C'\)là:
\(\dfrac{C_{ABC}}{C_{A'B'C'}}=\dfrac{3}{2}\)
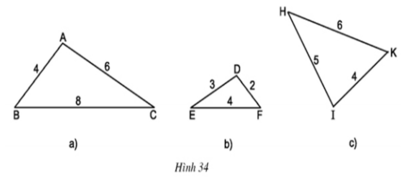
Ba cạnh ΔABC tương ứng tỉ lệ với ba cạnh ΔDFE
⇒ ΔABC ∼ ΔDFE