Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mỗi bài, mk làm một phần ví dụ cho cậu nhé
nó đối xứng với nhau qua pt đường thẳng đenta,
trường hợp (d) ko cắt (đen ta) hay (d) cắt (đen ta) thì đều làm theo phương pháp sau
lấy 2 điểm bất kì thuộc (d) thì ta có như sau: A(0:1) là điểm thuộc đường thẳng (d)
lấy A' đối xứng với A qua (đen ta)
liên hệ tính chất đối xứng qua đường thẳng thì hiểu là AA' vuông góc (đen ta)
đồng thời giao điểm của AA' với (đen ta) là trung điểm của AA'
dễ dàng tìm đc giao điểm của (đen ta) với (d) là K(-2/5;1/5)
từ pt (đenta) thì dễ dàng =) vecto pháp tuyến của (đenta) =) (3;-4)
vì AA' vuông góc với (đenta) nên =) vectơ pháp tuyến của AA' là (4;-3)
áp véctơ pháp tuyến của AA' vào phương trình tổng quát đc: 4(x-0)-3(y-1)=0 (=) 4x-3y+3=0
gọi I là giao điểm của AA' và (đenta) =) I(-6/7;-1/7)
mà I là trung điểm của AA'
chắc chắn cậu sẽ dễ dàng suy ra điểm A'
mà K và A' thuộc (d') nên dễ dàng =) phương trình của (d')

Đáp án C
+phương trình ∆ đi qua M (8; 2) và vuông góc với d là:
3 (x-8) +2(y-2) =0 hay 3x+2y -28= 0.
+ Gọi H = d ∩ ∆ ⇒ H ( 6 ; 5 )
+ Khi đó H là trung điểm của đoạn MM’. Áp dụng công thức trung điểm ta suy ra
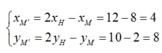
Vậy M’( 4;8) .

MH vuông góc với d
nên MH nhận vecto (2;-3) làm VTCP
=>VTPT là (3;2)
Phương trình MH là:
3(x+5)+2(y-13)=0
=>3x+15+2y-26=0
=>3x+2y-11=0
Tọa độ H là:
2x-3y=3 và 3x+2y=11
=>x=3 và y=1
Theo đề, ta có:
\(\left\{{}\begin{matrix}x_N+\left(-5\right)=2\cdot3=6\\y_N+13=2\cdot1=2\end{matrix}\right.\Leftrightarrow N\left(11;-11\right)\)

Bài 3:
Gọi M là giao điểm \(d_1;d_2\Rightarrow\) tọa độ M là nghiệm:
\(\left\{{}\begin{matrix}x+y-1=0\\x-3y+3=0\end{matrix}\right.\) \(\Rightarrow M\left(0;1\right)\)
Gọi \(A\left(1;0\right)\) là 1 điểm thuộc \(d_1\)
\(d_3\) đối xứng \(d_2\) qua \(d_1\Leftrightarrow d_1\) là phân giác góc tạo bởi \(d_2;d_3\)
\(\Rightarrow d_3\) qua M và \(d\left(A;d_3\right)=d\left(A;d_2\right)\)
Gọi pt \(d_3\) có dạng \(a\left(x-0\right)+b\left(y-1\right)=0\Leftrightarrow ax+by-b=0\)
Theo công thức khoảng cách:
\(\frac{\left|a.1+b.0-b\right|}{\sqrt{a^2+b^2}}=\frac{\left|1-3.0+3\right|}{\sqrt{1+3^2}}\Leftrightarrow\frac{\left|a-b\right|}{\sqrt{a^2+b^2}}=\frac{\sqrt{8}}{\sqrt{5}}\)
\(\Leftrightarrow5\left(a-b\right)^2=8\left(a^2+b^2\right)=3a^2+10ab+3b^2=0\)
\(\Leftrightarrow\left(a+3b\right)\left(3a+b\right)=0\Rightarrow\left[{}\begin{matrix}a=-3b\\b=-3a\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn:
\(\left[{}\begin{matrix}-3bx+by-b=0\\ax-3ay+3a=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}3x-y+1=0\\x-3y+3=0\end{matrix}\right.\)
Bài 2:
a/ Gọi d' là đường thẳng qua M và vuông góc d
\(\Rightarrow d'\) nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình d':
\(2\left(x-2\right)-1\left(y-5\right)=0\Leftrightarrow2x-y+1=0\)
H là giao điểm của d và d' nên tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x+2y-2=0\\2x-y+1=0\end{matrix}\right.\) \(\Rightarrow H\left(0;1\right)\)
b/ M' đối xứng M qua d \(\Leftrightarrow H\) là trung điểm \(MM'\)
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M\\y_{M'}=2y_H-y_M\end{matrix}\right.\) \(\Rightarrow M'\left(-2;-3\right)\)
c/ d' đối xứng d qua M \(\Rightarrow\) phương trình d' có dạng: \(x+2y+c=0\) với \(c\ne-2\)
Ta có: \(d\left(M;d\right)=d\left(M;d'\right)\)
\(\Leftrightarrow\frac{\left|2+2.5-2\right|}{\sqrt{1^2+2^2}}=\frac{\left|2+2.5+c\right|}{\sqrt{1^2+2^2}}\)
\(\Rightarrow\left|c+12\right|=10\Rightarrow\left[{}\begin{matrix}c=-2\left(l\right)\\c=-22\end{matrix}\right.\)
Phương trình d': \(x+2y-22=0\)
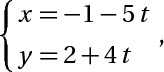 d2:
d2: 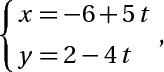
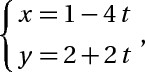 d2 : 2x+4y-10=0
d2 : 2x+4y-10=0
4 câu giống nhau, mình làm câu a, bạn tự làm 3 câu còn lại hoàn toàn tương tự:
a/ Đường thẳng d nhận \(\left(1;-2\right)\) là 1 vtpt
Gọi d' là đường thẳng qua M và vuông góc d \(\Rightarrow\) d' nhận \(\left(2;1\right)\) là 1 vtpt
Phương trình d':
\(2\left(x-4\right)+1\left(y-1\right)=0\Leftrightarrow2x+y-9=0\)
Gọi H là hình chiếu vuông góc của M lên d \(\Rightarrow\) H là giao điểm của d và d'
Tọa độ H là nghiệm: \(\left\{{}\begin{matrix}x-2y+4=0\\2x+y-9=0\end{matrix}\right.\) \(\Rightarrow H\left(\frac{14}{5};\frac{17}{5}\right)\)
Gọi M' là điểm đối xứng với M qua d \(\Rightarrow\) H là trung điểm MM'
Tọa độ M': \(\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=\frac{8}{5}\\y_{M'}=2y_H-y_M=\frac{29}{5}\end{matrix}\right.\) \(\Rightarrow M'\left(\frac{8}{5};\frac{29}{5}\right)\)
mình cảm ơn nhiều ạ