
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HN
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên

8 tháng 9 2023
\(y'=\dfrac{1}{3}\cdot3x^2-m\cdot2x+2m+3=x^2-2m\cdot x+2m+3\)
Để hàm số đồng biến trên R thì y'>=0 với mọi x thuộc R
=>Δ=(-2m)^2-4(2m+3)<=0 và 1>0
=>4m^2-8m-12<=0
=>m^2-2m-3<=0
=>(m-3)(m+1)<=0
=>-1<=m<=3
mà m nguyên
nên \(m\in\left\{-1;0;1;2;3\right\}\)
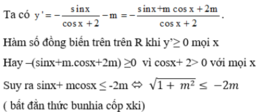
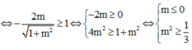
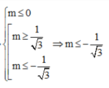
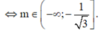
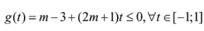
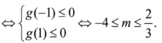


\(y=mx-\left(2m-3\right)cosx\)
\(y'=m+\left(2m-3\right)sinx\)
Để hàm số đồng biến trên \(ℝ\)thì \(y'\ge0\)với mọi \(x\inℝ\).
\(m+\left(2m-3\right)sinx\ge0\)với mọi \(x\inℝ\)(1)
Vì \(-1\le sinx\le1\)nên ta có:
Với \(2m-3\ge0\Leftrightarrow m\ge\frac{3}{2}\)thì
(1) tương đương với \(m-\left(2m-3\right)\ge0\)
\(\Leftrightarrow m\le3\)
suy ra \(\frac{3}{2}\le m\le3\).
Với \(2m-3< 0\Leftrightarrow m< \frac{3}{2}\):
(1) tương đương với: \(m+\left(2m-3\right)\ge0\)
\(\Leftrightarrow m\ge1\)
suy ra \(1\le m< \frac{3}{2}\).
Vậy ...